ESTA BIBLIOTECA DE MANIPULABLES VIRTUALES CORRESPONDE AL COMIENZO DE ESTE BLOG. (Se trata de aplicaciones antiguas que pueden presentar aspectos no adaptados a su perfecto funcionamiento online)
DURANTE AÑOS SE HAN IDO ACTUALIZANDO, MEJORANDO Y, SOBRE TODO, INTEGRANDO EN UNIDADES DIDÁCTICAS MÁS AMPLIAS,
EN LOS EXCEPCIONALES INSTRUMENTOS DE ENSEÑANZA-APRENDIZAJE QUE FORMAN EL ACTUAL PROYECTO MATE.TIC.TAC.
Dado que el proyecto MATE.TIC.TAC se comercializa en nuestra tienda online, comprenderán que no podemos ofrecer aquí parte de las aplicaciones individuales que las integran ni enlaces directos a las mismas como si se hizo antes, durante 10 años.
Este espacio, junto con Manipulables_Virtuales_Matemáticas_II, III y IV estará dedicado a mostrar una amplia colección de manipulables virtuales, para la enseñanza-aprendizaje de las matemáticas básicas, que he realizado hasta la fecha así como la incorporación de otros nuevos. Progresivamente se irán mejorando algunos de ellos para adaptarlos, si no lo están, a la PDI, o para mejorarles alguna función. Probablemente se trate de la colección, en Flash, más amplia, variada e interactiva que se puede encontrar en la red. Se facilita la URL de cada manipulable para que lo puedas incluir en tu página web o blog, si lo deseas.
Bajo la denominación de Manipulables se agrupan una serie de ayudas tanto físicas como virtuales que facilitan el aprendizaje.
Un Manipulable para matemáticas puede entrar en dos categorías:
1) Físicos, que se definen como cualquier material u objeto físico del mundo real que los estudiantes pueden “palpar” para ver y experimentar conceptos matemáticos. Los instrumentos de este tipo se utilizan principalmente con los estudiantes de los primeros grados escolares y ejemplos de ellos son: Formas Geométricas para el reconocimiento de las distintas figuras; Bloques de Patrones para estimar, medir, registrar, comparar; Bloques y Cubos para sumar, restar o resolver problemas que incluyen peso.
2) Virtuales, que se definen como representaciones digitales de la realidad posibilitadas por los computadores, y que el estudiante puede también manipular con el mismo objetivo de los primeros. Estos últimos se utilizan en los grados superiores. La experta Judy Spicer ha dicho: “Los manipulables virtuales tienen además la capacidad de hacer visible lo que es difícil de ver e imposible de imaginar” [1]. Ejemplos de éstos son: Simulaciones; Software de Visualización; Fractales; Robótica; Juegos de Computador; Representaciones Tridimensionales; etc.
(Tomado de "LOS MANIPULABLES EN LA ENSEÑANZA DE LAS MATEMÁTICAS", Eduteka)
---------------------------------------------------------------------------------------------------
Relación de manipulables
(se irá incrementando progresivamente):
I.- Formas y orientación en el espacio. Magnitudes geométricas:
----------------------------------------------------------------------------
Tangram chino. Traslación y giro.
Tangram chino virtual. Propone la formación de 14 figuras empleando, en cada caso, las siete piezas del tangram. Éstas se pueden desplazar y girar con las teclas de flecha. La pieza en forma de paralelogramo se puede, además, reflejar. Para facilitar la formación, se da la silueta de la figura propuesta a tamaño real. Sobre ella se llevan y se colocan las piezas.
----------------------------------------------------------------------------
Generador de figuras.
Generador de figuras propuestas que son combinación de cuatro formas básicas, cada una de ellas en cuatro posiciones diferentes. La figura propuesta se forma pulsando sobre cuatro de las 16 figuras-posiciones posibles. Sencilla aplicación para favorecer el desarrollo de la percepción analítica.
----------------------------------------------------------------------------
Taller de figuras.
Composición de diseños libres y propuestos a partir de colecciones sencillas de piezas de las que se pueden obtener tantas copias como se desee. Varios niveles de dificultad. Composición de formas complejas a partir de formas simples. Relaciones de reunión y multiplicidad. Percepción espacial, creatividad, etc...
----------------------------------------------------------------------------
Policubos.
Formación de estructuras y esculturas policúbicas a partir de cubos unitarios, semicubos, barras y placas que se presentan en dos perspectivas diferentes (isométrica y caballera). De cada poliedro unitario se pueden obtener tantas copias como se deseen. Varias pantallas o escenas diferentes.
----------------------------------------------------------------------------
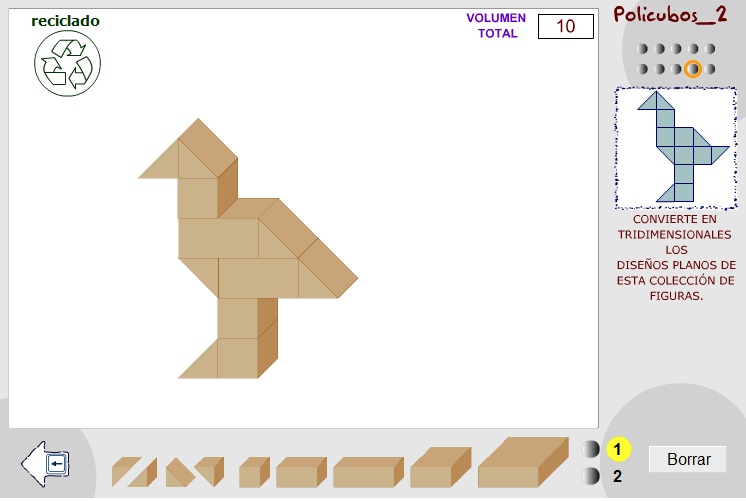
Policubos II.
Formación de estructuras y esculturas policúbicas a partir de cubos unitarios y semicubos en diferentes orientaciones espaciales. De cada poliedro unitario se pueden obtener tantas copias como se deseen, tanto en tamaño grande como en tamaño pequeño (mitad). La aplicación permite mostrar u ocultar interesantes propuestas de trabajo.
----------------------------------------------------------------------------
Marioneta.
Marioneta con movimiento realista. Cada uno de sus partes móviles puede rotarse tanto en el sentido de las agujas del reloj como en sentido contrario pulsando sobre ella o sobre el punto de articulación. La aplicación propone 10 posturas diferentes de la marioneta a modo de retos. Percepción espacial, estimación de ángulos, creatividad, etc...
----------------------------------------------------------------------------
Copiar figuras.
Copiar figuras dadas de manera que la original y la realizada coincidan mediante simple traslación.
Se proponen 16 figuras diferentes ( con dificultad creciente) que se presentan autodibujándose para así apreciar mejor la direccionalidad de los trazos. Lleva registro de figuras correctamente copiadas.
----------------------------------------------------------------------------
Trazado de polígonos regulares con la ayuda del semicírculo graduado.
Se ilustra, para el caso concreto del hexágono regular, cómo puede ser utilizado un semicírculo graduado (que puede ser girado) para trazar polígonos regulares una vez se ha determinado el valor angular del arco correspondiente al ángulo central del poligono...
----------------------------------------------------------------------------
Geoplanos.
La aplicación permite trabajar tanto con una trama ortométrica de puntos como con una trama isométrica. Los segmentos de línea se trazan pulsando sobre los puntos sensibles del geoplano. Además de con segmentos, se puede trabajar con una línea poligonal de número de segmentos variable, cada uno de ellos de longitud variable y con atracción a los puntos del geoplano...
----------------------------------------------------------------------------
Plantillas de ángulos fijos básicos.
Se utilizan triángulos equiláteros, cuadrados y escuadras ( mitades de cuadrados) como plantillas que incorporan ángulos fijos de valores básicos: 45º, 60º y 90º. Se proponen 4 colecciones diferentes de polígonos cuadroescuadrotriangulares (que pueden ser reproducidos con copias desplazables y girables de los tres polígonos básicos) para estudiar, por composición, los valores de cada uno de los ángulos interiores de los polígonos propuestos y para descubrir regularidades para la suma de los ángulos de un polígono en función de su número de lados...
----------------------------------------------------------------------------
Geoplano inteligente y resolución de problemas geométricos.
En una primera pantalla de aprendizaje por descubrimiento, el ordenador informa sobre la clase y características de cada uno de los polígonos trazados ( también sobre el área del mismo). En una segunda pantalla se propone la resolución, con corrección de la respuesta, de 20 retos consistentes cada uno de ellos en determinar, trazándola, una figura que cumpla los requisitos dados.
----------------------------------------------------------------------------
Poligonal + semicírculo - o círculo - graduado.
Poligonal que puede mostrar de 1 a 8 segmentos de longitud variable. Se muestra la longitud de cada segmento visible de la misma.
Son numerosísimas las posibilidades didácticas de esta poligonal en combinación con el círculo o el semicírculo graduado ( que pueden mostrarse u ocultarse). Estos últimos pueden rotarse. Además, el semicírculo graduado es desplazable y permite medir ángulos con gran precisión...
----------------------------------------------------------------------------
Perímetros.
Aplicación que propone la medición (mediante regla desplazable y girable o mediante segmento variable) de lados de polígonos (regulares e irregulares) para calcular sus perímetros. Se guía paso a paso, mediante un texto incompleto (con autocompletado inteligente mediante teclado), la comprensión y realización de los numerosos retos propuestos.
----------------------------------------------------------------------------
Perímetros II.
Aplicación que propone la formación de polígonos con un determinado perímetro. Para ello, se puede variar el número de lados del polígono así como la longitud de cada uno de ellos.
----------------------------------------------------------------------------
Escalera. Figuras isoperimétricas.
Permite ilustrar la equivalencia de perímetros de diferentes escaleras (con diferentes números de peldaños) que tienen en comun la distancia vertical y horizontal que deben salvar.
----------------------------------------------------------------------------
Bicicleta. La longitud de la circunferencia.
Permite medir la longitud y el radio de ruedas de diferentes tamaños que giran dejando como rastro un segmento de recta. Favorece el descubrimiento de un valor aproximado de "pi" a través de relación entre la longitud (L) medida, para una determinada rueda, y su diámetro (D). Esta relación se utiliza para expresar la fórmula de la longitud de cualquier circunferencia de diámetro ( o radio) conocidos...
----------------------------------------------------------------------------
Perímetros . Una propuesta internivelar.
Nueva aplicación resultado de la adaptación y mejora de algunas aplicaciones que habíar ealizado hace años y que, al contrario que ésta, no estaban adaptadas para su utilización con PDI. Rica en modelos dinámicos interactivos para visualizar el concepto de perímetro, familias de figuras isoperimétricas, perímetro de polígonos regulares y círculo,...). Como innovación más relevante, ofrece la posibilidad de explorar relaciones perímetro-área así como de asignar expresiones algebraicas a perímetros de figuras...
----------------------------------------------------------------------------
Áreas de figuras básicas y sus relaciones.
La nueva aplicación que se ofrece es el resultado de la adaptación y mejora de algunas aplicaciones que había realizado hace años y que, al contrario que ésta, no estaban adaptadas para su utilización con PDI.
(Incluye, mejoradas, algunas de las aplicaciones sobre cálculo de áreas que se relacionan a continuación)
La nueva aplicación que se ofrece es el resultado de la adaptación y mejora de algunas aplicaciones que había realizado hace años y que, al contrario que ésta, no estaban adaptadas para su utilización con PDI.
Se trata de una aplicación muy completa que ilustra, de manera dinámica, cómo se obtienen las áreas de figuras básicas (triángulo rectángulo, otros triángulos, paralelogramos, cometas, trapecios, polígonos regulares y círculo) a partir del área del rectángulo. También propone el cálculo estratégico de áreas de familias de figuras obtenidas en mallas cuadradas y en mallas triangulares equiláteras así como el área de las figuras básicas antes mencionadas.
En ella se le da un tratamiento especialmente interactivo al área de un círculo a partir del área de un polígono regular. Y al área de ambos a partir de la del rectángulo (también a partir de las áreas de paralelogramos y romboides).
(Incluye, mejoradas, algunas de las aplicaciones sobre cálculo de áreas que se relacionan a continuación)
----------------------------------------------------------------------------
Áreas de figuras planas.
La aplicación propone el cálculo de varias colecciones de polígonos: una formada por cuadrados más medios cuadrados, otra formada por triángulos equiláteros y mitades de los mismos; otra por figuras diversas obtenidas en una malla cuadrada y otra por diversas figuras obtenidas en una malla triangular equilátera. En unos casos se utiliza el cuadrado unitario como unidad de área y en otros el triángulo equilátero unitario.
----------------------------------------------------------------------------
Área de polígonos con vértices en una trama ortométrica.
La aplicación propone, para cada nuevo reto, trazar polígonos de tantos lados como se desee (tres como mínimo, evidentemente) cuyos vértices sean los puntos sensibles de una trama cuadrada u ortométrica ( polígonos de Pick) y que tengan un área dada (de manera aleatoria). Para un área dada, la aplicación permite guardar (para visualizar posteriormente) diferentes soluciones. Controla número de aciertos e intentos. Permite variar el colore de la figura, etc...
----------------------------------------------------------------------------
Área de polígonos con vértices en una trama isométrica.
Modo comprender y modo practicar. En el modo comprender se muestra el área del polígono trazado. El interior del polígono ( relleno) puede ser desplazado para comprender mejor su equivalencia en triángulos unitarios de la malla o trama ( unidades de área). En modo practicar, con cada nuevo reto, se propone la formación de un polígono de una determinada cantidad de área ( propuesta por el ordenador de manera aleatoria).
----------------------------------------------------------------------------
Área de polígonos con vértices en una trama isométrica II.
Una simple varfiante del manipulable anterior.
----------------------------------------------------------------------------
Triángulo dinámico. Área de un triángulo a partir del rectángulo circunscrito.
Pertmite variar los vértices de un triángulo ( que se ajustan a los vértices de una trama ortométrica). De manera interactiva se muestra el rectángulo que lo circunscribe. De esta manera, se puede calcular estratégicamente el área del triángulo restando al área del rectángulo circunscrito las áreas de tres triángulos rectángulos o bien de tres triángulos rectángulos y un rectángulo menor.
----------------------------------------------------------------------------
Áreas de figuras geométricas.
Manipulables para la comprensión de áreas de figuras formadas sólo por cuadrados unitarios, de rectángulos y cuadrados, de triángulos, de romboides, de cometas, de polígonos regulares. Aproximación al área del círculo. Presenta, para cada tipo de figura, retos relacionados con el cálculo de áreas. Completado automático. Lleva cuenta de intentos y aciertos. PDI: sí.
----------------------------------------------------------------------------
Triángulos. Clases.
Con cada nuevo reto, el ordenador propone la búsqueda de un triángulo de un determinado tipo (tanto en relación a las longitudes de sus lados como a los valores de sus ángulos interiores.
----------------------------------------------------------------------------
Composición hexagonal con escuadras.
Se muestra, paso a paso, cómo se puede utilizar una escuadra como plantilla para obtener, sobre papel, escuadras huecas que se pueden colorear y recortar. Con 36 de ellas se puede componer una estructura herxagonal en tamaño grande que puede ser utilizada para decorar las clase y para visualizar diferentes polígonos...
----------------------------------------------------------------------------
Pizarras geométricas.
Cuatro particiones del plano diferentes: con cuadrados, con escuadras mitades de cuadrado, con triángulos equiláteros y con triángulos rectángulos (1/6 de triángulo equilátero). Cada uno de los polígonos básicos de la partición puede "encenderse" o "apagarse" pulsando sobre él. Dos pizarras básicas tienen la opción de colorear de manera diferente cada uno de los polígonos básicos de la partición. De esta manera se pueden formar fácilmente figuras complejas por composición de figuras elementales, descubriendo, así, relaciones de reunión, de multiplicidad, etc...
----------------------------------------------------------------------------
Diseño mosaicos coloreando.
Jamás diseñar mosaicos fue tan rápido ni tan sencillo. La aplicación presenta tres pantallas diferentes que permiten el diseño de un sinfín de atractivos mosaicos. Basta elegir un color determinado, de la paleta de colores disponible, y pulsar sobre uno de los polígonos individuales de la pantalla para que este se rellene del color elegido. Para cada una de las diferentes pantallas (diferentes particiones poligonales del plano), la aplicación presenta varios modelos interactivos de mosaico.
Esta aplicación, además, se puede utilizar como PIZARRA PARA EL DISEÑO Y ESTUDIO DE FIGURAS (relaciones de reunión y multiplicidad, etc)
----------------------------------------------------------------------------

Diseño de mosaicos con teselas curvilíneas.
Para el diseño se utilizan 6 teselas básicas diferentes correspondientes a las 6 figuras isoperimétricas posibles con perímetro formado por cuatro cuadrantes de circunferencia del mimo radio. Permite la creación de una infinidad de diseños muy vistosos. Las piezas pueden rotarse, desplazarse y borrarse ( una a una o todas a la par). Presenta atracción entren piezas próximas para facilitar la exactitud y mayor belleza estética del diseño.
----------------------------------------------------------------------------

Algunos mosaicos de la Alhambra de Granada.
Visión dinámica de algunos mosaicos de la Alhambra de Granada realizados con las teselas "hueso", "clavo" (o "avión") y "pajarita".
----------------------------------------------------------------------------
Simetría.
Permite formar un sinfín de figuras con uno o dos ejes de simetría bilateral, a partir de una línea poligonal con número de lados configurable (de 1 a 8) y vértices desplazables.
----------------------------------------------------------------------------
Triángulos simétricos.
Por defecto, muestra dos triángulos simétricos con respecto a un eje de simetría bilateral. Los triángulos se presentan en movimiento (como una danza) y deformables, para apreciar dinámicamente el efecto de la simetría. También se puede detener el movimiento y desplazar los vértices del triángulo gris ( izquierda).
Hago simetría.
Con cada nuevo reto ( hay 20 diferentes), se propone que el usuario trace la figura simétrica a la dada. Permite la comprobación mediante rotación de la figura inicial sobre la figura realizada ( que será correcta si ambas se superponen). Lleva estadística de aciertos y fallos, etc...
Con cada nuevo reto ( hay 20 diferentes), se propone que el usuario trace la figura simétrica a la dada. Permite la comprobación mediante rotación de la figura inicial sobre la figura realizada ( que será correcta si ambas se superponen). Lleva estadística de aciertos y fallos, etc...
----------------------------------------------------------------------------
Simetría central o cíclica.
La aplicación permite obtener, de manera combinatoria, un sinfín de figuras con simetría central o cíclica.
----------------------------------------------------------------------------
Ejes de simetría. Permite tanto el diseño libre de figuras como la formación de figuras con un eje de simetría horizontal, con un eje de simetría vertical o con dos ejes de simetría perpendiculares. Permite verificar si la figura tiene las características de simetría correspondientes a la opción elegida. La formación de figuras se realiza pulsando sobre segmentos de una trama que pueden iluminarse o apagarse.
----------------------------------------------------------------------------
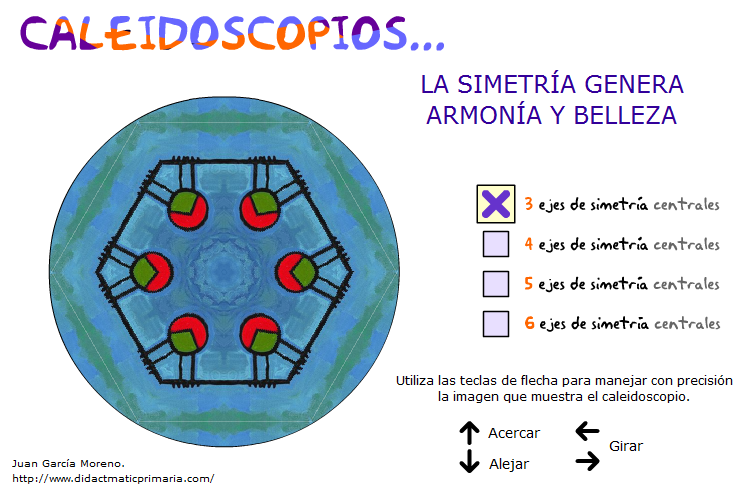
Caleidoscopios.
Una gratificante experiencia visual a partir de la formación de un sinfín de figuras con 3, 4, 5 ó 6 ejes de simetría centrales. Para cada opción elegida (número de ejes de simetría) el caleidoscopio toma vida moviendo el puntero del ratón sobre él o bien pulsando las teclas de flecha.
----------------------------------------------------------------------------
----------------------------------------------------------------------------
(Ver a pantalla completa)
----------------------------------------------------------------------------
Medir ángulos.
Con cada nuevo reto, la aplicación muestra un ángulo de amplitud angular aleatoria. La medición del ángulo (reto propuesto) se puede llevar a cabo bien con un semicírculo graduado o bien con un círculo graduado. Estos instrumentos pueden ser girados con las flechas de tecla con total precisión. La aplicación informa sobre lo correcto o no de la medida.
----------------------------------------------------------------------------
Polígonos regulares.
Visualización de polígonos regulares de diferente número de lados. Permite variar el radio del polígono regular, mostrar u ocultar sus diagonales ( así como la fórmula que permite obtener el número de éstas), mostrar u ocultar su ángulo central ( así como la información sobre el cálculo del valor del ángulo central e interior característico del polígono).
----------------------------------------------------------------------------
División de la circunferencia en arcos iguales y trazado de polígonos regulares. Resolución de retos propuestos.
Con cada nuevo reto, la circunferencia aparece dividida en un número aleatorio de partes (arcos) mediante puntos sensibles que son los extremos de los mismos. Se pide, en cada caso, pulsar sobre puntos que sean los vértices de un polígono regular de un número de lados dado (este número es, siempre, divisor del número de arcos en que se presenta dividida la circunferencia)...
----------------------------------------------------------------------------
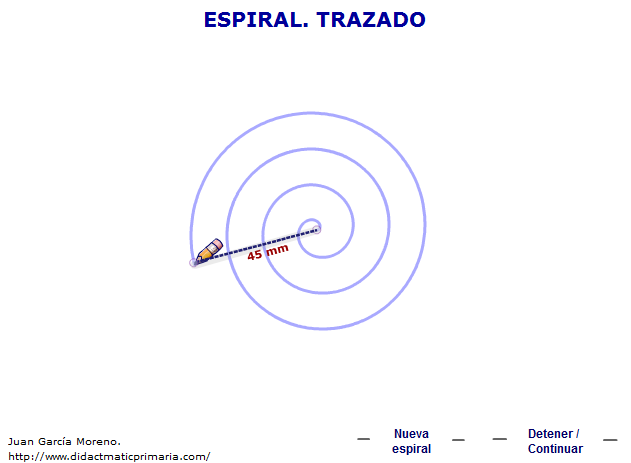
Espiral.
Simulación del trazado de una espiral mediante una cuerda de longitud creciente que gira alrededor de un punto fijo y tiene en su extremo un lápiz.
----------------------------------------------------------------------------
Pentominós.
Aplicación que permite utilizar tantas copias como se desee de cada uno de los 12 pentominós diferentes. Cada pieza se puede trasladar, girar, reflejar y borrar individualmente. La aplicación cuenta con 6 pantallas adicionales con información textual y gráfica que ilustran diferentes propuestas de trabajo con estas piezas (teselación, puzzles, etc...)
----------------------------------------------------------------------------
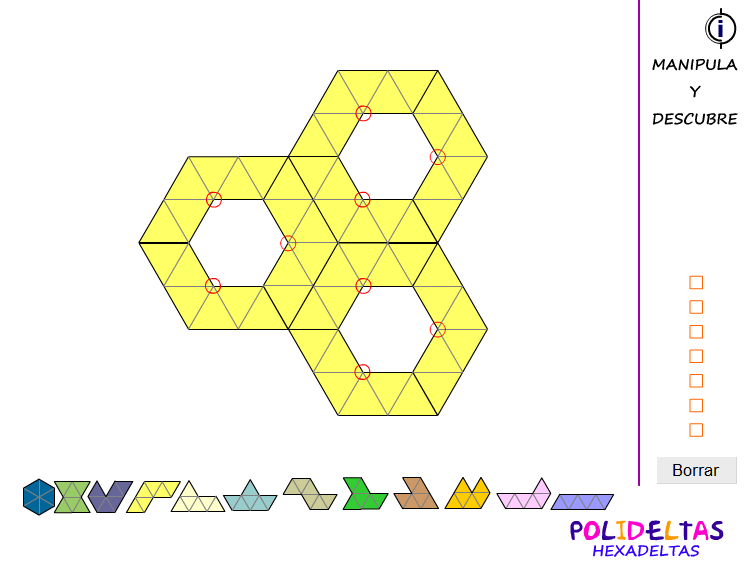
Polideltas. Diseño con hexadeltas.
Aplicación que permite utilizar tantas copias como se desee de cada uno de los 12 hexadeltas diferentes. Cada pieza se puede trasladar, girar, reflejar y borrar individualmente. La aplicación cuenta con 7 pantallas adicionales con información textual y gráfica que ilustran diferentes propuestas de trabajo con estas piezas (teselación, puzzles, etc...)
----------------------------------------------------------------------------
Rompecabezas rómbico con 12 hexadeltas.
Permite desbaratar el rompecabezas cambiando las piezas de posición y aplicando sólo traslación a las mismas o bien traslación y giro. Además, ofrece pantalla de diseño para los hexadeltas piezas del rompecabezas y la posibilidad de imprimir las piezas a tamaño mayor para realizar el puzzle a mayor escala.
----------------------------------------------------------------------------
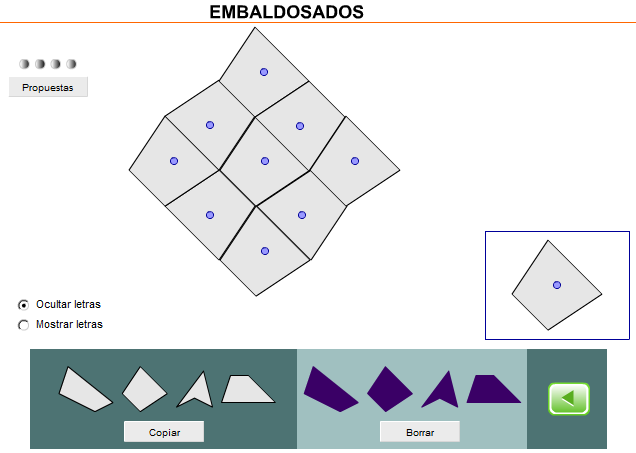
Embaldosados con triángulos y cuadriláteros.
Permite comprobar manipulativamente que cualquier triángulo tesela o embaldosa el plano. Idem para cuadriláteros (tanto convexos como cóncavos). La aplicación propone también descubrir las posibilidades combinatorias de la composición de dos o más triángulos (idem para cuadriláteros). Las piezas son desplazables y girables.
----------------------------------------------------------------------------
Cuadriláteros. Clases.
Al desplazar alguno/s de los vértices de un cuadrilátero cualquiera (que se ajustan automáticamente a los vértices de una cuadrícula) se forma un nuevo cuadrilátero. La aplicación, de manera automática e interactiva, informa sobre la clase (paralelogramo, trapecio, rectángulo, ...) del mismo describiendo, a la par, las características de sus lados y ángulos. Puede, también, mostrar el área de cada uno de los cuadriláteros formados.
----------------------------------------------------------------------------
Volumen de un ortoedro o caja.
Permite visualizar ortoedros y variar cada una de sus aristas (de 1 a 10 unidades de longitud). En la pantalla de aprendizaje se muestra, interactivamente, el volumen del ortoedro formado. En otra pantalla se propone como reto averiguar el volumen del ortoedro formado y comprobar la respuesta.
----------------------------------------------------------------------------
Ortoedros. (Ortoedros policúbicos)
Permite obtener ortoedros de diferentes dimensiones como composición de cubitos unitarios ( unidad de volumen) que pueden ser separados y desplazados. A partir de un ortoedro original de un determinado volumen se podrán formar múltiples estructuras policúbicas de igual volumen...
----------------------------------------------------------------------------
Ortoedros II. (Ortoedros policúbicos)
Una variante, con menos texto y sin dibujos de niños, del anterior.
----------------------------------------------------------------------------
Permite abrir y cerrar el desarrollo plano de cada uno de los cinco poliedros regulares (o sólidos platónicos) para su mejor percepción espacial. Además, una vez abierto un determinado poliedro, propone completar con números iguales los lados del desarrollo plano ( aristas del poliedro cerrado) que coinciden en una misma arista del poliedro cerrado, permitiendo comprobar si lo hemos hecho bien o no.
----------------------------------------------------------------------------
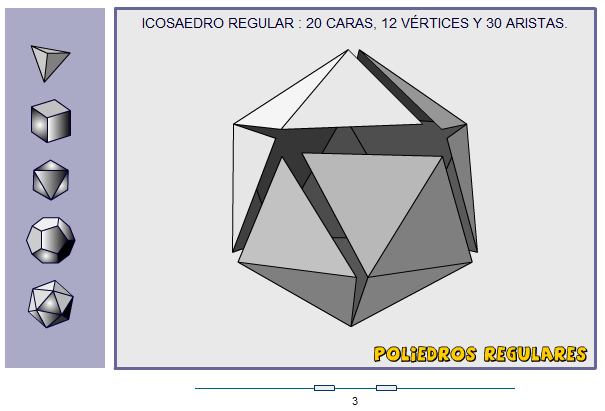
Poliedros arquimedianos y relación de Euler.
Permite visualizar más de 20 poliedros arquimedianos (los que tienen caras poligonales regulares) abriendo y cerrando sus correspondientes desarrollos planos. También permite determinar si se sabe averiguar el número de caras, vértices y aristas de cada uno de ellos.
----------------------------------------------------------------------------
3D_Poliedros.
Permnite visualizar, en perspectiva, las estructura alámbrica de diferentes poliedros: cubo, pirámide de base cuadrada, octaedro regular, pirámide no simétrica 1/3 de cubo, semicubo prismático, tetraedro regular, dodecaedro rómbico, cuboctaedro, dos tetraedros compenetrados, et... Los poliedros pueden ser rotados en el espacio y aumentar o disminuir su tamaño.
----------------------------------------------------------------------------
Desarrollos planos alternativos de algunos poliedros.
Permite visualizar diferentes desarrollos planos alternativos para un determinado poliedro elegido recolocando interactivamente sus caras en diferentes posiciones y orientaciones. Además, propone completar con números iguales los lados del desarrollo plano (aristas del poliedro cerrado) que coinciden en una misma arista del poliedro cerrado, permitiendo comprobar si lo hemos hecho bien o no.
----------------------------------------------------------------------------
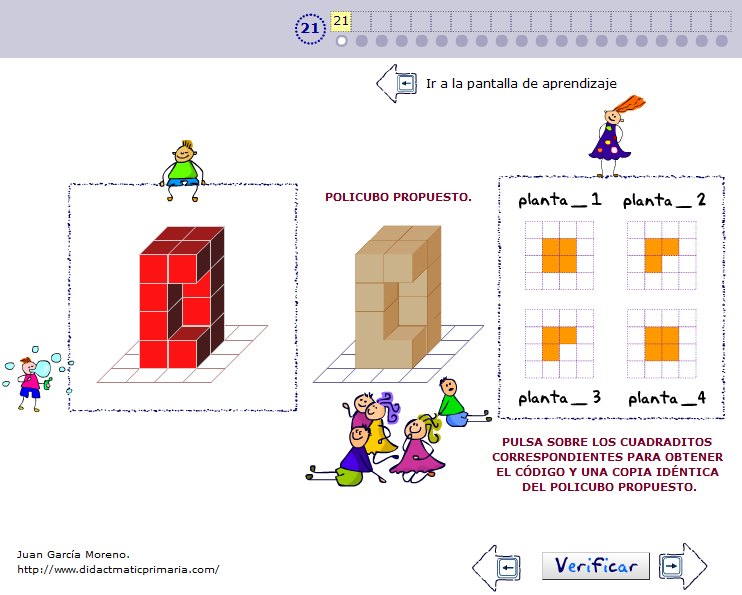
Presenta varias pantallas o escenas, tanto para manipulación libre como para resolución de múltiples retos propuestos. Permite el diseño/codificación de estructuras policúbicas con cuatro capas o plantas ( cada una de ellas dividida en 16 cuadraditos). Cada pulsación sobre un cuadradito determinado coloca un cubo (si no lo había) o borra (si ya había un cubito colocado) en la posición y capa correspondiente en la ventana de visualización. De esta manera es enormemente fácil diseñar la estructura policúbica deseada o propuesta...
----------------------------------------------------------------------------
Área de polígonos con vértices en puntos de una trama ortométrica. Teorema de Pick.
La aplicación permite trazar polígonos de tantos lados como se desee (tres como mínimo, evidentemente) cuyos vértices sean los puntos sensibles de una trama cuadrada u ortométrica ( polígonos de Pick) y calcular su área. Se ilustra, para cada caso, el cálculo del área aplicando la sencilla fórmula de Pick.
----------------------------------------------------------------------------
Triángulos posibles e imposibles.
Juego de tres barritas, de longitudes configurables, ancladas por sus vértices de manera que dos de ellas ( a y c) se pueden girar y hacer coincidir en un punto determinado, que será un vértice del triángulo si las longitudes de los lados cumplen la propiedad triangular...
Se puede variar fácilmente la escala del conjunto de la construcción así como desplazarla.
----------------------------------------------------------------------------
Problemas geométricos. (Cortar figuras)
Se proponen 20 problemas geométricos. Cada uno de ellos se resuelve "cortando" un polígono (en verde) de otro mayor (en rosa claro). En cada problema se da la relación ( para el área y el perímetro) del polígono menor con respecto al mayor. El polígono verde se genera pulsando sobre puntos sensibles del polígono mayor y puede separarse del mismo. Permite verificar la respuesta y llevar control de aciertos y problemas realizados.
----------------------------------------------------------------------------
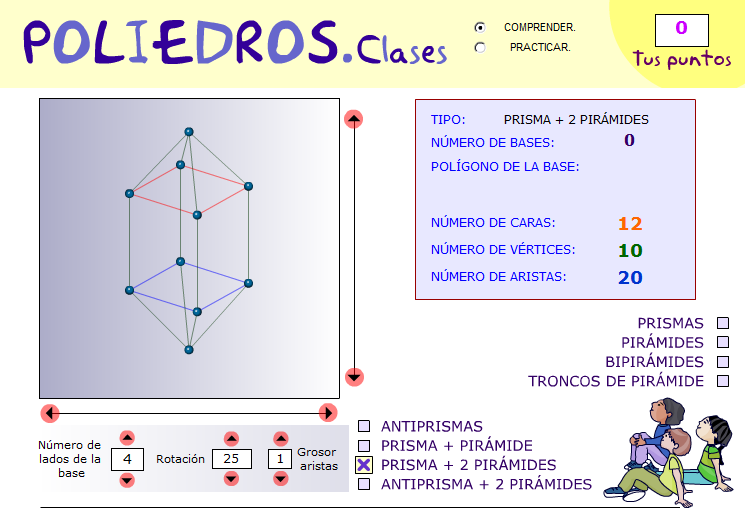
Poliedros. Clases.
Permite la visualización de prismas rectos, pirámides, bipirámides, troncos de pirámide, antiprismas, poliedros obtenidos como prisma + pirámide, prisma + 2 pirámides y antiprisma + 2 pirámides.
Los poliedros pueden girarse en el espacio. También se puede variar el número de lados de su base o sección, etc...
Los 8 manipulables que siguen son desagregaciones de éste.
----------------------------------------------------------------------------
Prismas.
Visualización de prismas rectos cuyas bases son polígonos regulares. Se puede variar el número de lados de los polígnos_bases, la altura del prisma, sus proporciones, girarlo en el espacio... incluso visualizarlo con "aristas" gruesas...
----------------------------------------------------------------------------
Pirámides.
Visualización de pirámides cuyas bases son polígonos regulares. Se puede variar el número de lados del polígono_base, la altura de la pirámide, sus proporciones, girarla en el espacio... incluso visualizarla con "aristas" gruesas...
----------------------------------------------------------------------------
Bipirámides ( o dipirámides).
Visualización de bipirámides resultantes de unir dos pirámides idénticas por sus bases (polígonos regulares). Se puede puede variar el número de lados del polígono_sección, la altura de la bipirámide, sus proporciones, girarla en el espacio... incluso visualizarla con "aristas" gruesas...
----------------------------------------------------------------------------
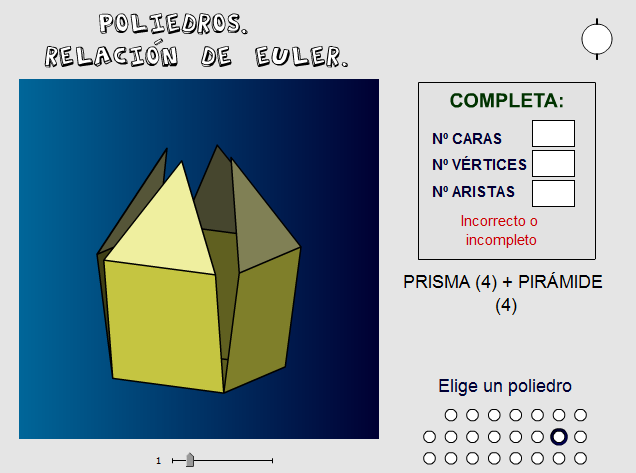
Prisma + pirámide.
Visualización de poliedros resultantes de unir un prisma con una pirámide por sus bases (polígonos regulares) coincidentes. Se puede puede variar el número de lados del polígono_sección, la altura del poliedro, sus proporciones, girarlo en el espacio... incluso visualizarlo con "aristas" gruesas...
----------------------------------------------------------------------------
Prisma + 2 pirámides.
Visualización de poliedros resultantes de unir un prisma con dos pirámides por sus bases (polígonos regulares) coincidentes. Se puede puede variar el número de lados del polígono_sección, la altura del poliedro, sus proporciones, girarlo en el espacio... incluso visualizarlo con "aristas" gruesas...
----------------------------------------------------------------------------
Troncos de pirámide.
Visualización de troncos de pirámide cuyas bases son polígonos regulares. Se puede variar el número de lados del polígono_base, la altura del tronco de pirámide, eltamaño relativo de las bases, girarlo en el espacio... incluso visualizarla con "aristas" gruesas...
----------------------------------------------------------------------------
Antiprismas.
Visualización de antiprismas cuyas bases (giradas entre sí) son polígonos regulares. Se puede variar el número de lados del polígono_base, la altura del antiprisma, sus proporciones, girarlo en el espacio... incluso visualizarlo con "aristas" gruesas...
----------------------------------------------------------------------------
Antiprisma + 2 pirámides.
Visualización de poliedros resultantes de unir un antiprisma con dos pirámides, todos ellos con bases poligonales regulares idénticas ( el octaedro y el icosaedro son dos casos particulares de esta clase de poliedros). Se puede variar el número de lados del polígono_base, la altura del poliedro, sus proporciones, girarlo en el espacio... incluso visualizarlo con "aristas" gruesas...
----------------------------------------------------------------------------
Secciones.
Permite visualizar ( por extrusión o levantamiento de secciones) prismas, pirámides, cuerpos con caras curvas, cuerpos redondos y sólidos de revolución a través de la superposición de secciones de los mismos ( de 0 a 100). Cada cuerpo geométrico puede ser visualizado como recto, curvo y oblícuo.
----------------------------------------------------------------------------
Sólidos de revolución.
Permite visualizar la generación de conos, cilindros y esferoides mediante la rotación, alrededor de un eje, de un triángulo rectángulo, un rectángulo y un semicírculo, respectivamente. Se puede variar tanto la perspectiva como la velocidad y sentido de la rotación.
(Ver a pantalla completa)
OTROS (Para ESO y Bachillerato)
----------------------------------------------------------------------------
Paralelismo y perpendicularidad de forma gráfica y analítica.
Relación entre las pendientes de rectas paralelas y perpendiculares.
----------------------------------------------------------------------------
Teorema de Thales.
Sistema de rectas desplazables en disposición "de Thales". Permite apreciar y comprobar la razón de proporcionalidad entre segmentos homólogos (y establecer proporciones) para cada una de las configuraciones concretas del sistema de rectas.
----------------------------------------------------------------------------
Comprobación gráfico-dinámica del Teorema de Pitágoras.
----------------------------------------------------------------------------
Puntos y rectas notables en un triángulo.
Completísima aplicación configurable que permite visualizar interactivamente alturas y ortocentro, medianas y baricentro, bisectrices e incentro, mediatrices y circuncentro, recta de Euler, circunferencias inscrita y circunscrita,...
----------------------------------------------------------------------------
Aproximación a la circunferencia mediante cuerdas envolventes.
----------------------------------------------------------------------------
Aproximación a la cardioide mediante cuerdas envolventes.
----------------------------------------------------------------------------
Aproximación a la nefroide mediante cuerdas envolventes.
----------------------------------------------------------------------------
Aproximación a la parábola mediante cuerdas envolventes.
----------------------------------------------------------------------------
Aproximación a la elipse mediante cuerdas envolventes.
----------------------------------------------------------------------------
Trazado de una elipse.
----------------------------------------------------------------------------
Hiperboloide hiperbólico.
----------------------------------------------------------------------------
Epicicloides.
Familia de EPICICLOIDES a partir de círculos con radios en proporción r/R = 1/n.
R: radio del círculo mayor (fijo)
r: radio del círculo pequeño (que rueda por el exterior del círculo grande)
r: radio del círculo pequeño (que rueda por el exterior del círculo grande)
----------------------------------------------------------------------------
Hipocicloides.
Familia de hipocicloides a partir de círculos con radios en proporción r/R = 1/n.
R: radio del círculo mayor (fijo)
r: radio del círculo pequeño (que rueda por el interior del círculo grande).
r: radio del círculo pequeño (que rueda por el interior del círculo grande).
----------------------------------------------------------------------------
Espirógrafo de dos brazos articulados.
Los brazos pueden girar en el mismo sentido (generando epicicloides) o en sentido contrario (generando hipocicloides). Se puede variar gradualmente la velocidad de rotación del conjunto, la de un brazo articulado con respecto al otro, el grosor del trazo, etc...
----------------------------------------------------------------------------
En el apartado dedicado a Geogebra para la Educación Primaria en este blog, podrás acceder a muchos otros manipulables realizados con Geogebra, como los incluidos en el Proyecto Gauss y los realizados por Daniel Mentrard.
Otro sitio que ofrece buen número de manipulables virtuales para la enseñanza de las matemáticas (grados preK-2, 3-5, 6-8 y 9-12) es ILLUMINATIONS, de la National Council of Teachers of Mathematics.
Otro de los sitios clásicos es la Biblioteca Nacional de Manipuladores Virtuales de la UtahState University:








































































No tengo palabras. Maravilloso. Gracias por compartir.
ResponderEliminarImpresionante trabajo, gracias.
ResponderEliminarMe parece extraordinario. Esto tiene que motivar a mis alumnos de 6º.
ResponderEliminarGracias por dedicar tanto tiempo. José Manuel
Esto sí son matemáticas y lo demás es cuento.
ResponderEliminarGracias, Anónimo, por tu comentario.
EliminarSin embargo, este enfoque de las matemáticas que no prioriza los contenidos sino las relaciones entre los diferentes bloques, las habilidades cognitivas y metacognitivas así como el desarrollo de competencias matemáticas, es asumido sólo por una minoría de docentes, justamente los que más formación tienen al respecto.
Un aporte educativo sensacional. Gracias
ResponderEliminarUn material muy bueno, gracias por compartirlo.
ResponderEliminarExcelente!!!!!!!!!un gran aporte
ResponderEliminarsencillamente exceleente, gracias por permitir trabajar con este material tan bueno atentamente fernando alfonso
ResponderEliminarPágina genial. Gracias por compartir el material.De Vicente Urquía.
ResponderEliminarGracias a todos por vuestros comentarios. En nuestras manos está contribuir a la mejora de la enseñanza-aprendizaje de las matemáticas básicas.
ResponderEliminarHola profe:
ResponderEliminarMil gracias por compartir tu trabajo con todos, es un placer poder acceder al mismo, para nosotros y para los críos.
¡¡ CLAS, CLAS, CLAS, CLAS, CLAS, CLAS, CLAS, CLAS, CLAS . . . ! ( Estos son aplausos )
Un saludo "agradecido".
Marian
Fantástico material y muy atractivo para los niños. Gracias por compartirlo.
ResponderEliminarGracias, Tania, por tu amable comentario. Saludos.
EliminarMuy buen material, gracias
ResponderEliminarMagnífico, grandioso, genial, fantástico, nunca hubiera imaginado la aplicación de las matemáticas.
ResponderEliminarGracias por compartir...
Muchas gracias, grovertapia, por tan elogioso comentario.
ResponderEliminarcomo descargo los manipulables
ResponderEliminarMuy bueno el trabajo, en primaria se han dedicado a primero y segundo grado, pero aquì he encontrado aplicaciones interactivas muy interesantes para 5to y 6to grado de primaria y temas que son complicados que el estudiante va a parender de manera creativa. Muy bueno.
ResponderEliminarExcelente trabajo.
ResponderEliminarSería bueno nos permita trabajar offline en nuestras escuelas donde no hay conectividad.
EXCELENTE, maravilloso trabajo y dedicación le será muy útil a mis alumnos millones de gracias
ResponderEliminarMe tienes fascinado por lo que haces y por la gran ayuda que nos aportas. Gracias.
ResponderEliminarGracias, Juan Manuel, por tu comentario. Seguro que te fascinará aún más mi próximo proyecto "COMPEMATETIC". Estoy trabajando a tope en el mismo.
EliminarSaludos.
Gracias, Juan Manuel, por tu comentario. Seguro que te fascinará aún más mi próximo proyecto "COMPEMATETIC". Estoy trabajando a tope en el mismo.
EliminarSaludos.
Simplemente apabullante.
ResponderEliminarHe encontrado lo que creo que es una errata. Se trata de la actividad "Geoplano inteligente y resolución de problemas geométricos". No consigo resolver el reto 4: https://goo.gl/Z3uPJY
Muchísimas gracias por compartir este material.
Gracias, Juan José por tu comentario y por el aviso de error. Efectivamente había una errata en la verificación del problema número 4 de la aplicación a la que aludes. ¡Ya está solucionado!
EliminarNuevamente, gracias.
Un cordial saludo.
¡Muchas gracias!
EliminarHola Juan y enhorabuena; el trabajo es impresionante. No recuerdo en los últimos años nada parecido en la creación de recursos digitales de matemáticas (Proyecto Gauss, Rekenweb, Proyecto Sur, NLVM, Proyecto Canals, Descartes...). Son magníficos y tu dedicación extraordinaria.
ResponderEliminar¿Te has puesto en contacto con alguien para poder traducirlos a euskera?
Un abrazo
Txerra
MUCHÍSIMAS GRACIAS POR HACER EVIDENCIAR ESTAS MARAVILLAS
ResponderEliminarHAN AYUDADO MUCHÍMO A MIS ESTUDIANTES
Gracias, Mauricio, por tu comentario. Me alegro de que te hayan resultado tan útiles.
EliminarSaludos.
Buen dia, gracias, bendiciones, excelente trabajo¡
ResponderEliminar¡Excelente trabajo! Felicidades.
ResponderEliminarBuenas tardes
ResponderEliminarGracias por los aplicativo, sabe que tengo un inconveniente porque ya no puedo utilizar los aplicativos cada vez que doy clic me llega un mensaje que ya no tiene soporte.
Me podrían informar que es lo que pasó?
Hola, Samuel.
EliminarEstos manipulativos ya no se ofrecen online. Están integrados dentro de otro proyecto más amplio, MATE.TIC.TAC, que ofrecemos en nuestra tienda para su uso offline.
Ve al inicio de este blog para ver lo que ofrecemos online de manera provisional.
Gracias.