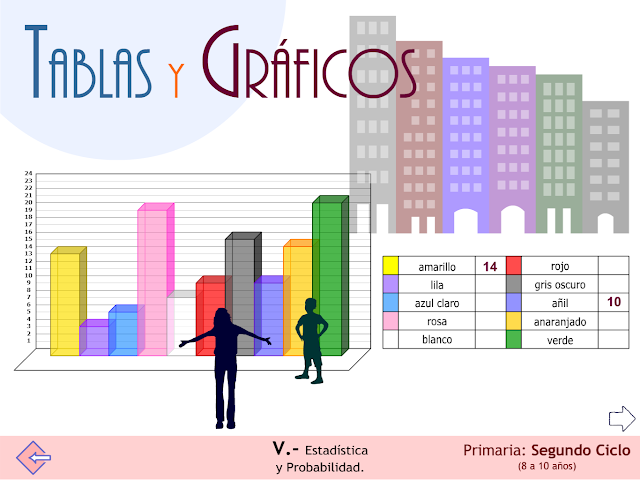
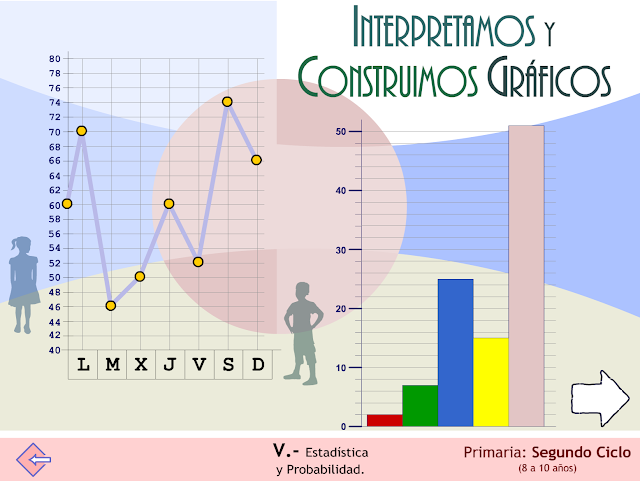
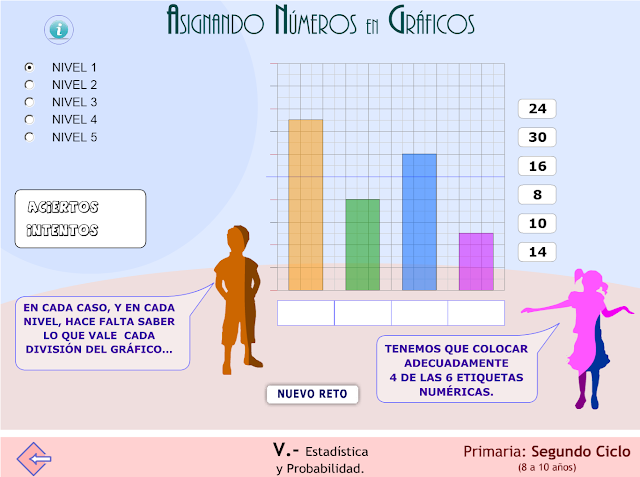
Tablas y gráficos

https://matetictac.com/

Recta numérica básica

Circuitos probabilísticos

Cálculo estratégico de productos y divisiones.

 

  Ver, también,

• Multiplicación (Kit interciclos)
• Formatos  interactivos para la enseñanza-aprendizaje de la división.
• Divisibilidad en Primaria
• Multiplicación y división. Algoritmos estándar.

Capacidad y volumen. Relaciones y equivalencias de unidades

Volumen y capacidad. Relaciones y equivalencia de unidades. Didactmaticprimaria.net

Las aplicaciones ofrecidas por DidctmaticPrimaria tienen, siempre, más potencial didáctico del que aparentan y sugieren sus títulos. Sirva ésta como ejemplo que ilustra la afirmación anterior. 

A partir de agrupaciones ortoédricas policúbicas ( formadas por cubos unitarios de un centímetro cúbico de volumen que se pueden recolocar como se desee) se facilita el descubrimiento de la fórmula que permite hallar el volumen de un ortoedro: largo x ancho x alto.

Además de la manipulación libre (espacio para favorecer el descubrimiento), las propuestas basadas en la generación aleatoria de ortoedros policúbicos permite proponer y resolver retos de cálculo mental multiplicativo (volumen del ortoedro dado).

Se utilizan las regletas de Cuisenaire (o números en color) para realizar agrupaciones ortoédricas de regletas del mismo valor (conexión números-geometría). Éstas se analizan desde el punto de vista de su volumen, a la vez que se estudian los desarrollos planos de las “cajas” abiertas asociadas a cada ortoedro como recipientes cuya área total y capacidad, en mililitros, hay que calcular (agrupaciones ortoédricas – desarrollos planos de ortoedros – recipientes ortoédricos – área total – volumen y capacidad)

De manera análoga a como se tratan los ortoedros policúbicos formados por cubos unitarios, se tratan los ortoedros formados por barras de 10 centímetros cúbicos o por placas de 100 centímetros cúbicos. Se llega, así, a una visión amplia y coherente de la descomposición del decímetro cúbico en 1000 cm³, 100 barra de 10 cm³ y 10 placas de 100 cm^3. (Hasta ahora sería como disponer de un decímetro cúbico desmontable y manipularlo desde diferentes puntos de vista…)

A partir del cubo de 1dm³, se construye un recipiente hueco de 1 litro de capacidad. Esto primero se asume como cierto y después se verificará de manera coherente. Se establecen las equivalencias dm³ ≡ litro,  cm³ ≡ mililitro, barra de 10 cm³ ≡ cl, placa de 100 cm³ ≡ dl y se procede a resolver retos consistentes en verter en  el recipiente cúbico (de 1 dm³), con la ayuda de un grifo, un vaso y una jeringa auxiliares, cantidades exactas de agua expresadas en diferentes unidades de capacidad o de volumen.

Pero no sólo llenamos el recipiente cúbico de agua de un grifo. Se utiliza como pluviómetro para establecer las relaciones especiales entre longitud, superficie, capacidad y volumen que permiten su correcto entendimiento. Relacionamos la “boca” de este recipiente (1 dm²) con un metro cuadrado (1 m²). Simulamos de manera realista la lluvia y el paso de tiempo acelerado. Se va registrando automáticamente la altura (en mm) del agua de lluvia , el volumen de agua de lluvia recogido en el recipiente cúbico, las precipitaciones  en litros/m²… Se observa que éste número es el mismo que el de milímetros de altura del agua en el recipiente… Se visualiza, se argumenta, se razona….

En definitiva, se facilita la enseñanza-aprendizaje de una matemática que conecta  e integra conceptos, que facilita enormemente su comprensión profunda favoreciendo la apreciación de patrones y regularidades en contextos matemáticamente relevantes, y realistas, gracias a la calidad visual e interactiva de los múltiples manipulativos que integra de manera innovadora y creativa.

 ¿Se puede ofrecer más en una aplicación de este tamaño?

Ver, también, 

• SMD-longitud, masa y capacidad