¿Cuántos topos ves? Infantil 4-5 años. (HTML5)

 

¿Cuántos topos ves? Didactmaticprimaria.net

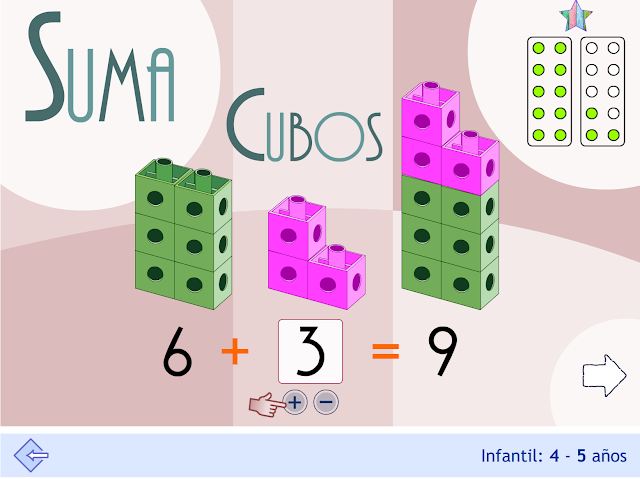
Otra aplicación para trabajar el 10. Son 10 las madrigueras de topos que se muestran en el paisaje. Al pulsar sobre una madriguera, aparece un topo. Al pulsar sobre un topo, éste se esconde. Con cada acción, un búho muestra el número total de topos visibles y se escucha el nombre del número. Esto facilita el conteo ascendente (suma) y descendente (resta) en el modo "búho".

En el modo "colibrís", con cada nuevo reto, se muestra aleatoriamente un número de topos (entre 0 y 10). Hay que escribir el número de topos visibles en cada caso. Si es correcto, se añadirá un nueva flor al paisaje. Los colibrís muestran el número introducido por el usuario.

Este contexto facilita la subitización directa (cuando el número de topos visibles es relativamente pequeño) y la subitización indirecta, o complementaria: cuando el número de topos es relativamente grande es más fácil percibir el número de madrigueras vacías. Dicho de otro modo, se puede calcular el número de topos visibles por subitización del número de madrigueras vacías (complemento al diez, amigos del diez)

Regletas de Cuisenaire para Infantil. (HTML5)

Regletas de Cuisenaire. Infantil 4-5 años. Didactmaticprimaria.net

Cuenta cubos. (Versión en HTML5)

 

(Código provisional: jgm123)

Pesa números. (Versión en HTML5)

 

(Código provisional: jgm123)

Haz tú otro igual. Y cuenta (versión en HTML5)

 

(Código provisional: jgm123)

Cubos de colores

 

Pulsar sobre la imagen para acceder a la versión online)

(Código provisional : jgm123)

Ábaco_contador configurable. Primer ciclo de Primaria (versión en html5)

 

(Código provisional: jgm123)

Tabla del 100 interactiva (versión en html5)

Suma cubos

Dada la extraordinaria acogida que está teniendo la aplicación Cuenta_cubos, y como complemento de la misma, aquí os ofrezco Suma_cubos. Espero que guste tanto como la anterior.

Obsérvese que en esta aplicación, al igual que en esta otra, 

se refuerza visualmente el modelo gráfico partes-todo. ¿Por qué este modelo es tan importante?

La investigación sobre problemas verbales aritméticos aditivos, desde diferentes enfoques, ha sido muy profusa y enriquecedora desde finales de la década de los setenta del siglo pasado. Actualmente son muchos documentos los que divulgan las conclusiones de Vergnaud y Durand (1976) o de Heller y Greeno (1979), entre otros …

Fruto de estas investigaciones, el profesorado cuenta con clasificaciones y secuenciación de categorías y tipos de problemas aritméticos verbales, en función de su estructura semántica, que muchos centros han ido incorporando al currículo de Matemáticas:

He aquí algunos buenos ejemplos de lo anterior:

Resolución de prolemas aritméticos. Eoep de Ponferrada.

Problemas aritméticos escolares. Ceip Ignacio Halcón. Lebrija.
Problemas aritméticos escolares. Metamodelos. Ceip Ignacio Halcón. Lebrija.

Si bien es importante tener en cuenta estas clasificaciones cuando elaboramos propuestas de resolución de PAEV, para no eludir ni olvidar categorías importantes y para tener en cuenta las que resultan más fáciles y más difíciles, no es menos cierto que debe ser esencial analizar el esquema mental que utiliza el resolutor cuando resuelve problemas de este tipo. Ni usted, ni yo, ni los/as alumnos/as tienen en cuenta para nada la clasificación anterior cuando resuelven un problema aritmético de estructura aditiva. Es obvio que, para resolverlo, no necesitan ni tienen que saber  si es de cambio, comparación, igualación… Es muy difícil saber cómo el/la niño/a procesa, transforma y traduce para sí la información en su cabeza…, Y es aquí, y desde la práctica en el aula, donde encuentro fundamental el esquema partes-todo, por su eficacia y sencillez y porque permite  integrar en torno al mismo todos los PAEV de nivel 1 y estructura aditiva.

Máquina "transforma_números". Cálculo estratégico.

Cuatro bolas se mueven dentro de un círculo por acción de fuerzas simuladas (gravedad, choque elástico,...). Con cada nuevo reto, las bolas toman unos valores numéricos iniciales (entre 1 y 5). Esos valores pueden cambiarse pulsando sobre una determinada bola y lanzándola, para que choque, contra un operador. Cuando el choque se produce, el valor antiguo de la bola se actualiza según lo indicado en el correspondiente operador ( se resta uno, se duplica, se añaden cinco unidades...). El cambio de valor numérico en cada bola se produce siempre y cuando no genere números negativos ni un valor de la bola mayor o igual que 100.

El número de bolas siempre es cuatro. El número de operadores cambia según el "nivel" de dificultad elegido.

El objetivo es conseguir la SUMA FINAL propuesta. Se facilita el objetivo mostrando, en todo momento, el valor de la SUMA ACTUAL (suma de los números de la bolas). El/la alumno deberá calcular mentalmente la diferencia SUMA FINAL - SUMA ACTUAL  y elegir estratégicamente una secuencia operacional, sobre una o varias bolas, que lleve a la solución. Esto lo obligará a retener resultados parciales (los/as alumnos/as con más facilidad para ello son los/as mejores en cálculo mental) y a no perder de vista el objetivo. Pero esta no es la única estrategia general que se puede seguir. Otra estrategia general podría ser descomponer, desde el inicio, la suma final en cuatro sumandos, y tratar de alcanzar en cada bola uno de estos sumandos,...

Los operadores que maneja esta aplicación son sencillos: -1, x2, :2, +5, x10. Para cada nuevo reto, los valores iniciales de las bolas, así como la suma final propuesta, se generan aleatoriamente dentro de unos rangos numéricos prefijados.

Se trata de una situación abierta, divergente...Por tanto, facilita el descubrimiento y aplicación de numerosas estrategias diferentes de cálculo para conseguir el objetivo.

Dos calculadoras con pocas teclas. Retos.

Acorde con el especial tratamiento que tienen las operaciones combinadas en las propuestas de Didactmatic, se ofrece esta otra aplicación que es una variante de una propuesta ya clásica: la formación de determinados números combinando operaciones y un limitado conjunto de teclas o valores numéricos en una calculadora.

El enfoque más corriente es proponer al alumnado operaciones combinadas para que llegue al valor numérico de las mismas siguiendo un determinado orden operacional. Este es un proceso totalmente convergente.

Aquí, por el contrario, la búsqueda de un resultado (convergencia) es un proceso totalmente abierto o divergente, creativo, ya que el espacio de búsqueda (el conjunto de todas las soluciones posibles) es muy amplio. Los/as alumnos/as construyen las operaciones combinadas que llevan a la solución y comprueban sus hipótesis. Todo ello con ayuda de unas calculadoras que registran y muestran la secuencia de números y signos tecleada.

Los números propuestos son generados aleatoriamente dentro de un rango y se establecen cuatro grados o niveles de dificultad. (Se han cambiado con fecha posterior al de su publicación)

Más sobre operaciones combinadas:

• En busca del significado. Operaciones combinadas en Primaria. ¿Por qué? ¿Para qué?
• UDI. Método de resolución de PAEV mediante el modelado algebraico con etiquetas de texto.

La numeración romana (2º y 3º ciclo de Primaria)

Nunca antes  había realizado una aplicación digital interactiva para tratar la enseñanza y aprendizaje de la numeración romana. 

Incluso en el tratamiento de un tópico como éste hay cabida para la creatividad y la innovación tecnológico-pedagógica. 

Una seña de identidad de las aplicaciones de Didactmatic es que no se eluden esfuerzos en el código de programación de la aplicación si ello revierte positivamente en calidad y excelencia, en una mejor  interactividad y en un mayor grado de generalización de lo tratado. La manipulación interactiva y "aumentada", el descubrimiento, la generalización y la excelencia al servicio de la enseñanza y aprendizaje de la matemática.

Recta numérica básica

Números enteros

Regletas de Cuisenaire. Versión digital.

Son muchos los vídeos , documentos teóricos y prácticos ("Trabajamos con las Regletas") que ilustran el interés y potencial didáctico de los "Números en color" de Cuisenaire, y relativamente numerosas las versiones digitales que se han hecho de las regletas.

He sido reticente durante años a realizar una versión digital de las regletas de Cuisenaire, sobre todo porque ya existían otras versiones. Curiosamente, todas las versiones que he encontrado, en las que las regletas se pueden desplazar, se basan en la representación plana de las mismas. No sé si esto se ha hecho así intencionadamente por parte de los desarrolladores, en atención a características psicológicas específicas de las edades de los alumnos a los que se destinan, o bien para eludir las dificultades técnicas añadidas que conlleva la representación tridimensional. Me temo que esto último ha tenido más peso en el diseño... Personalmente, yo sólo encuentro ventajas en la representación tridimensional de las regletas. Ésta ha sido una de las principales razones que me ha motivado a realizar esta aplicación, al constatar que existía espacio para la innovación y la mejora…

Me voy a centrar aquí exclusivamente en un análisis somero y crítico de estas versiones digitales desde el respeto y la consideración que merecen sus autores. Con el enfoque implementado en mi trabajo  “Evaluación de Contenidos Educativos Digitales Multimedia _ Matemáticas (CEDMMat)”, todas ellas pueden ser analizadas a la luz del modelo TPACK, es decir, desde el punto de vista de los diferentes grados de intersección o integración, logrados por los desarrolladores de estas versiones digitales, entre tecnología, didáctica-pedagogía y contenidos para asegurar una implementación exitosa de las TIC, entendiendo y aceptando que La tecnología optimiza (o puede optimizar) los procesos de enseñanza-aprendizaje con una compleja interconexión de tecnología, contenidos y pedagogía.

No descubro nada al afirmar que las regletas de Cuisenaire son un excelente material didáctico para la enseñanza-aprendizaje de las matemáticas, o al afirmar que se trata de un material polivalente. En el ámbito de las versiones digitales esto ha sido muy bien recogido en la aplicación “regletas”, de José Antonio Cuadrado. Se trata de una aplicación muy completa en este sentido. Ilustra cómo pueden utilizarse las regletas para trabajar múltiples conceptos, dada la polivalencia del material. Quizá haya descuidado aspectos como la manipulación libre, ya que no se pueden borrar regletas colocadas, no se ha contemplado la atracción a la cuadrícula y las regletas de las cuales se extraen copias ocupan demasiado espacio de la pantalla de trabajo….

La mayoría de los desarrolladores ha optado por realizar versiones elementales que contemplan exclusivamente la manipulación libre permitiendo obtener y colocar copias en pantalla, una a una, de las diferentes regletas. Éstas pueden presentar dos orientaciones: horizontal y vertical. Generalmente se contempla la atracción o ajuste a una cuadrícula (visible o invisible) para facilitar la colocación y exactitud en la composición realizada. He aquí algunas aplicaciones con las características descritas, todas ellas muy parecidas entre sí:

• La versión digital desarrollada por Ángel Martínez Recio (Universidad de Córdoba. España) tiene un diseño excesivamente elemental. La manipulación resulta poco atractiva al utilizar regletas muy pequeñas y muy pocas opciones de configuración. Resulta una aplicación pobre atendiendo a aspectos multimedia y a su interactividad.
• Algo análogo se puede decir de "Regletas de Cuisenaire con Geogebra" realizada por José Manuel Infante. Ni tan siquiera permite clonar regletas. Y es que Geogebra es un muy buen software pero resulta muy limitado cuando se pretende utilizarlo como Flash...
• La versión digital de NRICH enriching mathematics facilita el giro de las regletas pero hay que elegir siempre regleta antes de colocarla. Al igual que la anterior, no facilita el clonado de regletas del mismo valor y tiene muy pocas opciones de configuración.
• http://www.escolovar.org/mat_numero_cuisenaire1.swf. Prácticamente igual a las anteriores.
• NumBlox, de Math Toybox. Con respecto a las anteriores, añade la posibilidad de escribir en pantalla.
• De la aplicación Mathbars, de MathPlayground, he tomado el modo de elegir el valor de la regleta.
• En un nivel básico de diseño se encuentra también la versión para JClic  realizada por Miren Garralda. Es también muy limitado su potencial didáctico-pedagógico. Se centra en la asociación regleta color - número simbólico, ordenar de menor a mayor, sumar1, descomposiciones alternativas de números sencillos…Todo ello de manera cerrada sin posibilidad de que los niños manipulen con las regletas.
• La versión de learningmath aporta modo libre y propone, además, algunos problemas. Facilita el clonado de regletas del mismo valor, por simple pulsación, y su colocación en la pantalla de trabajo. Representa un avance con respecto a las anteriores.

En otro nivel más avanzado de diseño nos encontramos con aplicaciones tales como:

• El Proyecto Medusa ofrece “Los números que suman 10” y “Las sumas dobles”. La primera es bastante mejor desde el punto de vista del diseño multimedia que desde el punto de vista de su potencial didáctico-pedagógico. Considero que se ha realizado un gran esfuerzo para el tratamiento de un contenido muy específico y reducido a través de una propuesta excesivamente cerrada, dirigida y convergente, sin contemplar la manipulación libre….La segunda aplicación comparte características con la primera. Presenta regletas  tridimensionales pero sin la posibilidad de que el alumno realice acciones con ellas. Se utilizan para ilustrar la fase gráfica previa a la realización de actividades simbólicas (con números y signos) que son el verdadero objetivo de la aplicación.
• Vedoque nos ofrece una versión digital de las regletas con una manipulación no demasiado ágil debido a que no facilita el clonado de piezas del mismo valor y porque las piezas, mientras se desplazan, se ajustan a la cuadrícula. Eso causa el efecto de un desplazamiento discontinuo. Además de la manipulación libre, ofrece 20 interesantes puzles planos. Las regletas nunca presentan el símbolo numérico correspondiente a su valor ni las divisiones en regletas unitarias (blancas), aunque sí se facilita el recuento de unidades de cada una de ellas.
• Las muy conocidas regletas realizadas por  Gil Gijón Canal, David Cantos Vila y Maximina Fernández Orviz son una aplicación muy completa y elaborada. Muy equilibrada en sus aspectos téncicos y didáctico-pedagógicos. Como única pega, encuentro que, en modo jugar,  propone actividades de completar con valores numéricos que necesitan hacer uso del teclado, con lo que no se adaptan a la pizarra digital al requerir un teclado auxiliar. En este modo, la manipulación no resulta ágil debido a que no facilita el clonado de piezas del mismo valor.
• Como ya indiqué anteriormente, las regletas de José Antonio Cuadrado son una aplicación muy completa. Ilustra cómo pueden utilizarse las regletas para trabajar múltiples conceptos, dada la polivalencia del material. Ha cuidado mucho las explicaciones, mediante vídeos. Quizá haya descuidado aspectos como la manipulación libre, ya que no se pueden borrar regletas colocadas, no se ha contemplado la atracción a la cuadrícula y las regletas de las cuales se extraen copias ocupan demasiado espacio de la pantalla de trabajo…

Encontramos, también, interpretaciones más libres de las regletas y otras aplicaciones derivadas:

• La versión de la National Library of Virtual Manipulatives, Utah State University es más libre dado que no “respeta” la correspondencia color-longitud propia de las regletas Cuisenaire. Aunque contempla sólo la manipulación libre, permite clonar regletas numéricas de un determinado valor con mucha facilidad…
• MultipleRepresentations utiliza la regleta unidad y la decena entre otros tipos de representaciones…
• Fraction bars no utliza las regletas Cuisenaire pero sí “fraction bars” para trabajar las fracciones de una manera muy ágil y eficaz. Si la relaciono aquí es como pretexto para afirmar que aunque las regletas Cuisenaire sean muy polivalentes y permitan ilustrar numerosos conceptos, conviene utilizar, también, diferentes materiales para ilustrar-modelar un mismo concepto. Sería tremendamente aburrido, y poco creativo, utilizar las regletas para todas aquellas situaciones en que resultan adecuadas. 

........................................................................................................

He desarrollado la aplicación "Regletas de Cuisenaire" que ofrezco en este post teniendo en cuenta las virtudes y defectos, a mi juicio, de las anteriormente relacionadas. He pretendido en todo momento hacer rica la configuración de posibilidades en cada uno de sus modos de funcionamiento. He considerado prioritario enriquecer las posibilidades en el modo manipulación libre, favorecer el descubrimiento a través de una manipulación que resulte ágil y atractiva facilitando enormemente el clonado de regletas del mismo valor...

El cubo como unidad de diseño tridimensional ya lo había utilizado anteriormente en otras aplicaciones tales como ortoedro, Generación y codificación de policubos por capas,... La utilización del cubo unitario y de la regleta decena en bloques base 10 también son precedentes de esta aplicación. De análoga manera, he utilizado regletas (sin respetar los valores y colores de las de Cuisenaire) en varias aplicaciones que he realizado sobre fracciones.

Invito a los lectores a que descubran el potencial de esta aplicación y a que me hagan llegar las sugerencias que estimen oportunas.

Precio total de la compra y diferencia de precios. Suma y resta contextualizadas a partir de 2º de Educación Primaria.

(Ver a pantalla completa)

Bloques base 10. SND, suma y resta.

Hace ya casi un año que mi estimado colega Pepe Vidal  (de la Sociedad Canaria de Profesores de Matemáticas Isaac Newton) me manifestó que echaba en falta, entre todas mis aplicaciones, alguna dedicada a la suma/resta con bloques base 10...Y me animaba para que la desarrollara...

Tengo que confesar que sentía cierta pereza a hacerlo, previendo las dificultades, con el código de programación, con que me iba a encontrar. Bueno, por fin la he desarrollado y tengo que decir que me satisface el resultado final. 

Dado que en las escenas correspondientes a la suma y a la resta se ofrece un registro interactivo de los pasos realizados ( paso a paso o de manera simplificada) que no es sino un algoritmo natural y flexible para realizar la operación, puede que en un futuro la amplíe con la práctica de dichos algoritmos (ya en la fase puramente simbólica) puestos de manifiesto con la manipulación.

(Aplicación ampliada con fecha 29-10-2014)

He decidido no incluir escenas dedicadas a la multiplicación y la división porque tendrían que reducirse forzosamente a casos muy concretos y sencillos (doble, triple,...división entre 2, 3, 4...) que no suponen una suficiente generalización,  obligando, además,  a reducir progresivamente el tamaño de los elementos móviles hasta hacerlo poco estético y operativo... Además, el hecho de que un mismo material sirva para ilustrar diferentes conceptos no significa que sea el más idóneo, ni el único, para ilustrar esos conceptos. Es conveniente ilustrar un mismo concepto con materiales diferentes. No obstante, a continuación ofrezco unos enlaces a vídeos en los que se ejemplifica el cálculo del doble, el reparto entre 3, etc...

En los siguientes vídeos ,y en otros de arriba, se afirma o se da por sentado que en la resta (por detracción, o por comparación) hay que comenzar a "quitar siempre por las unidades". Se trata de una afirmación general que es contraria a la didáctica de la aritmética mental basada en números en la que las operaciones se realizan de izquierda a derecha poniendo de manifiesto de manera más rápida y clara un valor aproximado de la solución. Así, por ejemplo, 435 - 248 = 235 - 48 (hemos quitado 2 centenas tanto al minuendo como al sustraendo y ya se aprecia que la solución va a ser un valor en torno a 200) = 205 - 18 (hemos quitado 3 decenas tanto al minuendo como al sustraendo) = 200 - 13 = 197 - 10 = 187. 

Esto se pone de manifiesto perfectamente cuando representamos con los bloques tanto el minuendo como el sustraendo. Y sigue siendo perfectamente válido cuando partimos únicamente de la representación del minuendo y detraemos "por partes" el sustraendo.

En los siguientes documentos, de Jesús Javier Jiménez y Teodoro Yupa, respectivamente, se teoriza y se ilustran  un buen número de estrategias de cálculo mental.

http://docentes.educacion.navarra.es/jjimenei/downloads/estrategiascmental.pdf

Multiplicación basada en números

Esta macroaplicación, realizada en Flash, presenta fallos de compatibilidad al ser presentada actualmente mediante Ruffle. Dado que son tantas las aplicaciones diferentes que se enlazan en ella y dado que actualmente las mismas están perfectamente adaptadas, mejoradas e  integradas en otras aplicaciones dentro del proyecto MATE.TIC.TAC, he decidido que no merece la pena gastar esfuerzos en actualizarla. De cualquier manera, puede dar una buena idea de lo que publiqué en su momento.

                                       (Juan García Moreno, marzo-2022)