Los/as alumnos/as de Primaria resuelven ecuaciones sencillas desde el primer curso de Primaria, si bien éstas no se presentan (en libros y otros formatos impresos) en el lenguaje algebraico habitual (en el que las cantidades desconocidas se representan mediante letras). Una ecuación (de primer grado) es una IGUALDAD en la que aparece una cantidad incógnita cuyo valor se desea averiguar.
Es evidente que una ecuación puede expresarse en los lenguajes usuales: oralmente ("¿Por cuánto hemos de multiplicar 5 para obtener 20?", ¿Qué número hay que restar a 25 para obtener 17?",...); por escrito; de forma gráfica, de forma gráfico-numérica, etc...
No cabe duda de que los/as alumnos/as de Primaria están capacitados para resolver no sólo ecuaciones de primer grado sino sistemas de dos ecuaciones con dos incógnitas e incluso sistemas de múltiples ecuaciones con múltiples incógnitas. La cuestión fundamental es cómo se aborda didáctica y metodológicamente este contenido. Lo deseable es llegar a dominar el lenguaje algebraico, el más universal de todos los lenguajes. Lo ineludible, pues estamos hablando de enseñanza-aprendizaje de la matemática, es el razonamiento.
En este vídeo se ilustra cómo se introduce el álgebra (con el uso tradicional de la "x") para resolver una ecuación, en un contexto de resolución de problemas, en 3º de Primaria.
Es evidente que una ecuación puede expresarse en los lenguajes usuales: oralmente ("¿Por cuánto hemos de multiplicar 5 para obtener 20?", ¿Qué número hay que restar a 25 para obtener 17?",...); por escrito; de forma gráfica, de forma gráfico-numérica, etc...
No cabe duda de que los/as alumnos/as de Primaria están capacitados para resolver no sólo ecuaciones de primer grado sino sistemas de dos ecuaciones con dos incógnitas e incluso sistemas de múltiples ecuaciones con múltiples incógnitas. La cuestión fundamental es cómo se aborda didáctica y metodológicamente este contenido. Lo deseable es llegar a dominar el lenguaje algebraico, el más universal de todos los lenguajes. Lo ineludible, pues estamos hablando de enseñanza-aprendizaje de la matemática, es el razonamiento.
En este vídeo se ilustra cómo se introduce el álgebra (con el uso tradicional de la "x") para resolver una ecuación, en un contexto de resolución de problemas, en 3º de Primaria.
A mí me parece un tanto artificioso, por innecesario, que una niña de 3º de Primaria emplee el procedimiento formal tradicional para eludir los denominadores en la resolución de ecuaciones, es decir, multiplicar un ente tan abstracto como lo es toda una igualdad por el denominador. Parece más natural y coherente averiguar el valor correspondiente a la mitad (10 - 4 = 6) y aplicar el concepto de doble (doble y mitad se construyen apoyándose el uno en el otro) para averiguar el valor correspondiente a la cantidad entera. De esta forma se haría uso del razonamiento proporcional, que todo niño/a posee en mayor o menor grado, y cuyo desarrollo es esencial para lograr competencia en razonamiento numérico.
De cualquier manera, para mí, la cuestión didáctica fundamental que se puede analizar en este vídeo tiene que ver con la forma de representación. Bruner consideraba tres tipos de representación (enactiva, icónica y simbólica) y propuso que los conceptos se enseñasen siguiendo estas tres fases de forma que respondiesen de manera directa a los modos hipotéticos de representación. Dicho de otra manera, la forma en que los seres humanos se representaban mentalmente los actos, los objetos y las ideas, se podía traducir a formas de presentar los conceptos en el aula...
De cualquier manera, para mí, la cuestión didáctica fundamental que se puede analizar en este vídeo tiene que ver con la forma de representación. Bruner consideraba tres tipos de representación (enactiva, icónica y simbólica) y propuso que los conceptos se enseñasen siguiendo estas tres fases de forma que respondiesen de manera directa a los modos hipotéticos de representación. Dicho de otra manera, la forma en que los seres humanos se representaban mentalmente los actos, los objetos y las ideas, se podía traducir a formas de presentar los conceptos en el aula...
Tradicionalmente se ha venido utilizando, antes que la representación simbólica, la representación icónica - sobre todo el modelo gráfico de balanza/s - como forma de hacer más intuitivos, más atractivos y comprensivos - y más ajustado a las características psicológicas de los niños - los problemas algebraicos, así como para el desarrollo de la argumentación lógico-numérica y prealgebraica:
La imagen superior izquierda corresponde a un manipulable virtual que podemos encontrar en ILLUMINATIONS. La imagen superior derecha está tomada de Juan D. Godino y Vicenc Font en "Razonamiento algebraico y su didáctica para maestros" La imagen de la derecha muestra una propuesta realizada por GenMagic así como una imagen correspondiente a la aplicación "Pesa Pensando_1", incluída en mi trabajo multimedia "ProblemáTICas Primaria".
Las balanzas con funcionamiento realista presentan la ventaja añadida de que, con ellas, no sólo se dota de significado al equilibrio (=) sino a los desequilibrios (> y <) o, lo que es lo mismo, permiten abordar ecuaciones e inecuaciones.
Estas imágenes ponen de manifiesto relaciones que los/as niños/as de Primaria pueden interpretar y formular en forma de ecuaciones o igualdades. La correcta expresión de las mismas, así como del proceso de resolución, es ya una actividad prealgebraica interesante que interrelaciona expresión oral, argumentación lógica y razonamiento matemático.
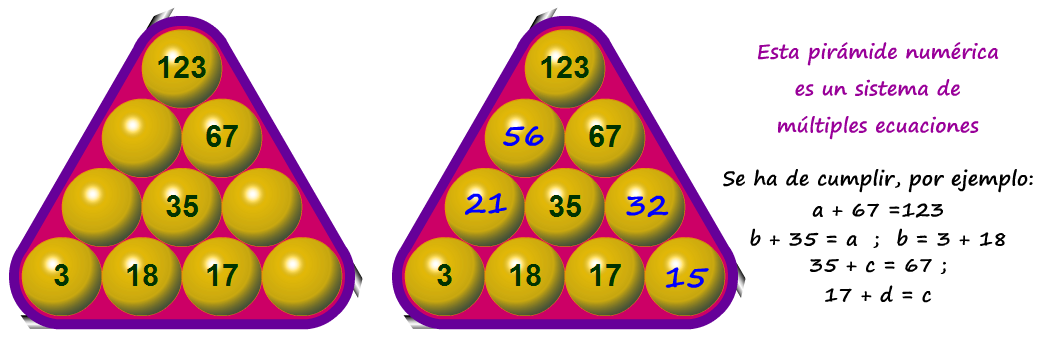
Las pirámides numéricas ( en este caso el número de cada bola debe ser la suma de los números de las bolas inferiores con las que contacta) no sólo permiten trabajar de manera atractiva la suma/resta sino estrategias de resolución relacionadas con el orden de los pasos a seguir.
En una fase prealgebraica de resolución de ecuaciones o sistemas de ecuaciones los/as alumnos/as verbalizan los pasos de la resolución (que encuentran totalmente lógicos y comprensibles con el "andamiaje" gráfico) que luego se van a corresponder con los pasos tradicionales que "dicta" la teoría clásica de resolución de ecuaciones...
Estas imágenes, tomadas por los propios alumnos/as con sus ultraportátiles, corresponden al aprovechamiento, en 6º de Primaria, de las aplicaciones interactivas "Pesa Pensando _1" y "Pesa Pensando _2" (dependiendo del nivel da cada alumno/a) para la resolución de ecuaciones y sistemas de ecuaciones en su fase algebraica escrita (justamente en la primera sesión dedicada a ello).
Los/as alumnos/as utilizan, para nombrar las incógnitas, las iniciales de los nombres de los objetos cuyo peso quieren averiguar. De esta manera, las incógnitas representan objetos concretos y no parámetros variables.
"La utilización de representaciones icónicas permite introducir en la educación primaria un tipo de razonamiento que se puede calificar de algebraico, pre-algebraico o casi-algebraico, y que no sería posible realizar en el caso de haber optado por una representación completamente simbólica"
(Juan D. Godino y Vicenc Font en "Razonamiento algebraico y su didáctica para maestros")
Algunos profesores de Secundaria están utilizando "Pesa Pensando 1" y "Pesa Pensando_2" de la misma forma que yo acabo de ilustrar para el tercer ciclo de Primaria. He aquí una nueva aplicación (especialmente diseñada para PDI) que utiliza bastantes de las imágenes de las aplicaciones aludidas, en la opción balanza fija. Permite resolver los retos propuestos, de manera pre-algebraica, realizando trazos para dibujar líneas, flechas, rodear, tachar, anotar cantidades,...
(Esta aplicación en Flash, en su versión antigua, tal y como se muestra aquí, no se encuentra perfectamente adaptada para ser mostrada mediante Ruffle ( sobre todo los textos), pero se puede encontrar mejorada en el proyecto MATE.TIC.TAC.)
Otro contexto prealgebraico interesante es el de las relaciones numéricas usuales. Imaginemos que una niña le dice a un niño: "Entre los dos tenemos 40 euros". Si nos preguntamos por la cantidad de dinero que puede tener cada uno de ellos, pronto caemos en la cuenta de que se trata de un problema abierto, divergente, con muchas soluciones posibles...
Efectivamente, se trata de una situación abierta porque algebraicamente toma la forma de la ecuación de una recta: x + y = 40. Como sabemos, cada punto de la recta es una solución diferente. Teóricamente habría infinitas soluciones que hacen cierta la ecuación. En nuestro caso, al solucionarla con los valores concretos asociados a los diferentes billetes y monedas del euro, imponemos restricciones a la ecuación y el número de soluciones posibles es ya finito, aunque elevado si se consideran soluciones con céntimos de euro (números decimales).
Los/as alumnos/as encuentran rápidamente una primera solución, casi siempre equitativa, el par (20,20). Parece como si resolvieran la cuestión como un problema de suma (simple combinación) a partir del recuerdo de hechos numéricos básicos (20 + 20 = 40). Pronto algún alumno descubre que niño y niña no tienen que tener necesariamente la misma cantidad de dinero. A partir de ese momento, comienzan a solucionar el problema como posibles descomposiciones del número 40 en dos números naturales (22,18); (30,10); (10;30); ertc... No tardan mucho en descubrir que hay muchísimas soluciones no enteras: (19.5,20.5); (2.8,37.2); (2.75,37.25); etc...
Efectivamente, se trata de una situación abierta porque algebraicamente toma la forma de la ecuación de una recta: x + y = 40. Como sabemos, cada punto de la recta es una solución diferente. Teóricamente habría infinitas soluciones que hacen cierta la ecuación. En nuestro caso, al solucionarla con los valores concretos asociados a los diferentes billetes y monedas del euro, imponemos restricciones a la ecuación y el número de soluciones posibles es ya finito, aunque elevado si se consideran soluciones con céntimos de euro (números decimales).
Los/as alumnos/as encuentran rápidamente una primera solución, casi siempre equitativa, el par (20,20). Parece como si resolvieran la cuestión como un problema de suma (simple combinación) a partir del recuerdo de hechos numéricos básicos (20 + 20 = 40). Pronto algún alumno descubre que niño y niña no tienen que tener necesariamente la misma cantidad de dinero. A partir de ese momento, comienzan a solucionar el problema como posibles descomposiciones del número 40 en dos números naturales (22,18); (30,10); (10;30); ertc... No tardan mucho en descubrir que hay muchísimas soluciones no enteras: (19.5,20.5); (2.8,37.2); (2.75,37.25); etc...
La descomposición numérica del número 40 en dos sumandos implica asignar una cantidad, x, cualquiera (x <= 40) a uno de ellos y averiguar luego la otra cantidad, y, de manera que y = 40 - x. Así, pues, cuando los/as niños hacen descomposición numérica están encontrando soluciones concretas de una ecuación, aunque los/as maestros/as de Primaria casi nunca seamos conscientes de ello.
A formas más complejas de expresar relaciones numéricas, corresponden problemas con ecuaciones más complicadas que no obstante los/as alumnos/as resuelven de manera prealgebraica:
A formas más complejas de expresar relaciones numéricas, corresponden problemas con ecuaciones más complicadas que no obstante los/as alumnos/as resuelven de manera prealgebraica:
En este caso, la ecuación implícita en el problema que hay que resolver , es x + 1 = y - 1, que equivale a x - y = -2, o a y - x = 2. Dicho de otro modo, cualquier solución en que la niña tenga 2 € menos que el niño será correcta...(Incluso a algunos adultos nos sorprende que una diferencia de 2 unidades entre los elementos de dos conjuntos se convierta en igualdad cuando se pasa una unidad de un conjunto a otro y, sin embargo, eso es lo que ocurre cuando, sin ir más lejos, pedimos a un/a alumno/a que descomponga el número 10 - con 10 lápices, por ejemplo- en dos grupos pasando, cada vez, un lápiz de un grupo a otro: De (4, 6) se pasa a (5, 5) ...)
He aquí una aplicación que provoca la necesidad de descomponer números en un contexto de resolución de problemas relacionados con formas usuales de expresar relaciones numéricas entre dos cantidades.
(Esta aplicación en Flash, en su versión antigua, tal y como se muestra aquí, no se encuentra perfectamente adaptada para ser mostrada mediante Ruffle ( sobre todo los textos), pero se puede encontrar mejorada en el proyecto MATE.TIC.TAC.)
Las actividades de geometría han sido tradicionalmente, también, fuente de interesantes situaciones para la introducción del álgebra
Esta imagen resume un tipo de actividad que siempre propongo a los/as alumnos/as ( en 5º o en 6º de Primaria). Les pido que, con la ayuda de una trama ortométrica, encuentren todos los polígonos "recortables" (por no utilizar lo de conexos) que son composición de cuatro escuadras (mitades de cuadrado) congruentes ( misma forma y tamaño) unidas de manera que compartan lados iguales...
Obtienen, así, una colección o familia de figuras equivalentes en área ( = dos cuadrados unitarios) pero con diferentes perímetros. Se les pide que codifiquen o expresen algebraicamente el perímetro de cada una de las 14 figuras de la colección utilizando los dos valores básicos "a" y "b" correspondientes a las longitudes del lado y diagonal del cuadrado unitario, respectivamente.
Obsérvese que en la expresión del perímetro "a" y "b" son "objetos concretos" (longitudes concretas de segmentos) y que en el contexto del problema planteado no actúan como parámetros variables. A partir de la observación directa y de la constatación de la relación "a < b", se puede pedir a los/as alumnos/as que comparen, por ejemplo, los perímetros de las figuras 10 y 11 y argumenten por qué la figura 10 tiene mayor perímetro que la 11...
---------------------------------------------------------------------------------
Este artículo tiene su continuación en Álgebra y resolución de ecuaciones en Primaria_2.













Que bien explican
ResponderEliminarMe gustan mucho sus planteamientos y me interesa bastante el tema. Además considero que tienen un buen soporte, el cual me ayudará mucho en mi investigación.
ResponderEliminarMuchas gracias.
Gracias por vuestros comentarios. Saludos.
EliminarGracias por vuestros comentarios. Saludos.
EliminarInteresante, me servirá para un trabajo. Lo tendrás en PDF?
ResponderEliminarMuy buena explicación
ResponderEliminarDe las mejores aportaciones para matemáticas que he leído.
ResponderEliminar