 |
| Esculturas con cubos y fracciones de cubo |
La imagen de la izquierda corresponde a la aplicación "policubos" que se ofrece en este blog. Pone de manifiesto correspondencias entre diseños figurativos planos formados por cuadrados y medios cuadrados (escuadras) y diseños figurativos tridimensionales formados con cubos y mitades de cubo. La aplicación ayuda a intuir y comprender el paso del plano (2D) al espacio tridimensional (3D) abordando, a la par, el diseño creativo...
En la aplicación "policubos II" se profundiza en el diseño libre con cubos y mitades de cubo con diferentes orientaciones espaciales.
Aplicaciones como "Copiar figuras" son ideales para el desarrollo de la percepción analítica que, como ya indiqué en un post anterior, es a la geometría lo que la comprensión lectora es a la lectura. Esta percepción analítica está favorecida por la referencia visual de la cuadrícula e implica la interiorización progresiva de aspectos topológicos, métricos y geométricos que no se pueden obviar. Ya en otros post he tratado con profundidad el potencial didáctico de cuadrícula y tramas de puntos para abordar múltiples contenidos geométricos a lo largo de toda la etapa Primaria: "Regularidades en el plano. Mosaicos, cenefas, celosías,..", "Tramas de puntos, geoplanos y pizarras geométricas",...
El libro "Materiales para construir la geometría" (de Claudi Alsina, Carme Burgués y Josep Mª Fortuny. Colección "Matemáticas: cultura y aprendizaje", número 11. 1988) comienza con un párrafo que yo he citado ya en diferentes sitios que, a mi juicio, orienta la didáctica de la Geometría en la escuela y en el que creo firmemente:
"Vivir la Geometría en la escuela puede ser una experiencia feliz si basamos su aprendizaje en actividades constructivas, sensibles y lúdicas. De todas las disciplinas matemáticas la Geometría es la que mayores posibilidades ofrece a la hora de experimentar, mediante materiales adecuados, sus métodos, sus conceptos, sus propiedades y sus problemas. Es por ello que la enseñanza geométrica no debe sucumbir a las limitaciones formales, simbólicas y algebraicas de los conocimientos matemáticos: será precisamente es este primer estadio de sensibilidad donde el tacto, la vista, el dibujo y la manipulación permitirán familiarizar al alumno con todo un mundo de formas, figuras y movimientos sobre el cual asentar posteriormente los modelos abstractos"
Pero, además, a través de las formas, figuras y movimientos el alumno se adentra en un terreno de estética, de belleza,...sensaciones que, casi sin excepción, a todos nos produce esa especial perfección y armonía que percibimos en múltiples formas geométricas.
No cabe, duda, por tanto, de que el tratamiento de la geometría, sobre todo de la geometría construida por los alumnos, incide de lleno en la educación en valores: si bien el reconocimiento y sentimientos de la armonía y belleza en relación con sus propias producciones geométricas tiene una componente subjetiva (y por tanto hay que desarrollar también esa sensibilidad) para el alumno, por otra parte éste asume con facilidad que el grado de exactitud, armonía y belleza tiene una componente objetiva que está directamente relacionada con su interés y esfuerzo por lograr perfección en el trazado y construcción de formas, ...
 No cabe duda de que las TICs, en conjunción con multitud de software específico de geometría dinámica, están facilitado enormemente una visión creativa, dinámica e interactiva de la Geometría que no era posible, o al menos muy difícil, hace relativamente pocos años. Este hecho trae consigo, de manera ineludible, nuevos enfoques e innovaciones del currículo de geometría, también a nivel elemental.
No cabe duda de que las TICs, en conjunción con multitud de software específico de geometría dinámica, están facilitado enormemente una visión creativa, dinámica e interactiva de la Geometría que no era posible, o al menos muy difícil, hace relativamente pocos años. Este hecho trae consigo, de manera ineludible, nuevos enfoques e innovaciones del currículo de geometría, también a nivel elemental.
Pero en Primaria no resulta fácil acercar a los alumnos/as el mundo de lo tridimensional, mediante aplicaciones virtuales, de manera que suponga para ellos una experiencia que conlleve, además, aprendizaje relevante. No al menos en la misma medida que para las figuras planas. No resulta nada fácil, por ejemplo, realizar diseños tridimensionales con Geogebra o algún otro software parecido. ¿Qué aplicaciones virtuales permiten a alumnos/as de Primaria la composición/descomposición de cuerpos tridimensionales? Nos tenemos que conformar con facilitarles la visualización de poliedros y estructuras poliédricas, incluso mostrarles poliedros que se transforman en sus correspondientes desarrollos planos, y viceversa; pero poco más...
He aquí algunas de las aplicaciones que se ofrecen en este blog que permiten trabajar diferentes aspectos de sólidos tridimensionales:

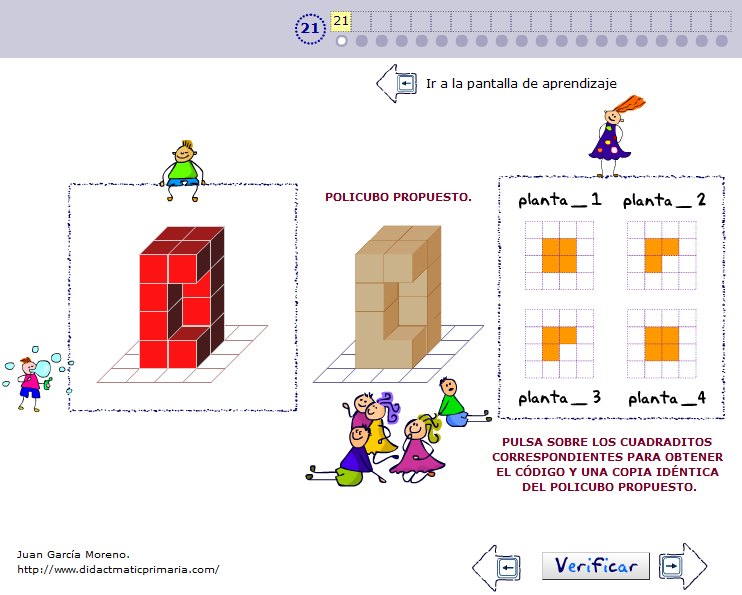
+

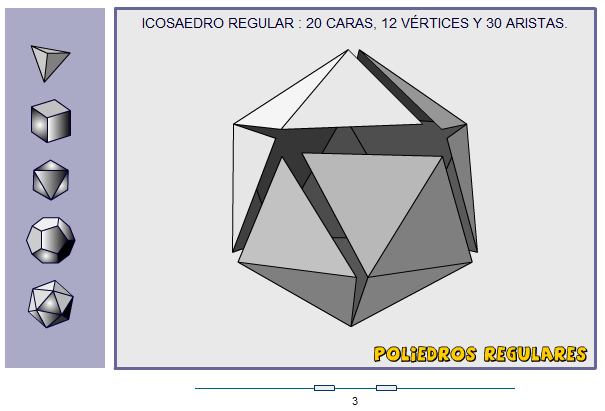
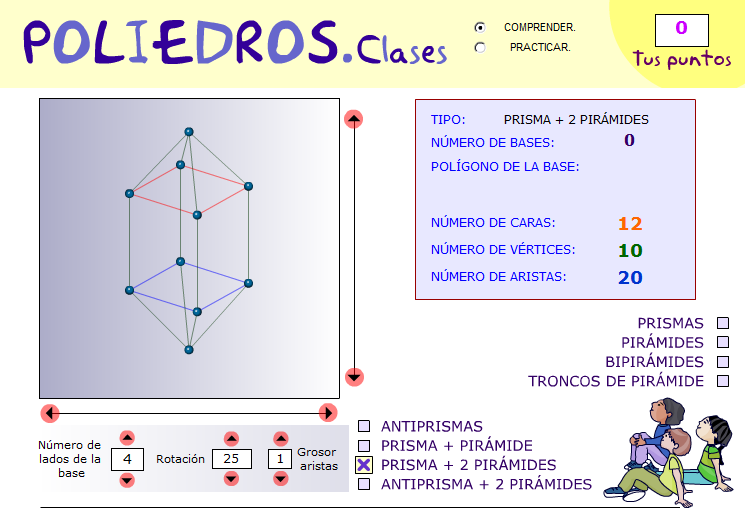 Fraccionamientos del cubo y su relación con otros sólidos platónicos (numerosos applets realizados con CabriJava)
Fraccionamientos del cubo y su relación con otros sólidos platónicos (numerosos applets realizados con CabriJava)
A pesar de lo variado de estas aplicaciones y del indudable interés didáctico que supone la manipulación de modelos ya construidos, es necesario proponer a nuestros alumnos/as otras actividades "analógicas", de índole constructiva, manipulativa y lúdica que hagan uso de los procedimientos fundamentales de la Geometría: el dibujo y la construcción de modelos. Actividades que los ayuden a desarrollar y adquirir dominio en el trazado, doblado, recortado, pegado, construcción, etc; que desarrollen actitudes de perseverancia y afán de superación...
En el siguiente vídeo recojo algunas de las actividades de este tipo que he propuesto yo a alumnos/as de 5º y 6º. Podéis consultar, también, "Origami modular en Primaria". Espero que las encontréis interesantes y sugerentes:
Quiero acabar este post saltando de lo básico de esta temática, a lo más avanzado . Lo que nos muestra el siguiente vídeo es impresionante, alucinante,...
Inspirado por la división celular, Michael Hansmeyer escribe algoritmos que diseñan formas y figuras con millones de facetas extremadamente fascinantes. Ninguna persona podría delinearlas a mano, pero son construibles, y podrían revolucionar la manera en la que concebimos la forma arquitectónica.






Hola Juan, magnífica entrada, las actividades interactivas nos vienen estupendamente para las sesiones de inclusión dedicadas a la geometría. En mi cole, que según parece, es menos internauta que el tuyo, trabajamos mucho con materiales y recursos manipulables, aparte de que en estas etapas (infantil y primaria)es imprescindible,entre ellos "VOLUMES A CONSTRUIRE", de Fernand Nathan, igual lo conoces, por si acaso no, te lo recomiendo.
ResponderEliminarHace unos días compartí una de las sesiones del trabajo con geoplanos (inclusión en 3º),aunque falta parte del proceso, da una idea de cómo lo hacemos.
Saludos
Saludos
Gracias, Alicia por tu comentario. No conocía la obra de Fernand Nathan. Ya he investigado algo sobre la misma y guardado algunos documentos en formato .pdf. Está muy bien enfocada didácticamente.
ResponderEliminarSaludos.
Estimado Juan. Me ha parecido excelente el recurso interactivo de desarrollo de diferentes poliedros, y de hecho lo he recomendado entre la comunidad de docentes de mi país (Uruguay), pero te cuento que lamentablemente desde hace un tiempo nos está dando error el enlace. ¿Podríamos recuperarlo de alguna manera? Muchas gracias desde ya. Saludos desde Montevideo, Esther Moleri.
ResponderEliminarEstimada Esther. Desde hace más de un año, los recursos digitales e interactivos que se ofrecían en este blog de manera gratuita, abierta y online, ya no se sirven así( a excepción de los últimos recursos publicados en este blog, en HTML5 que se ofrecen con un código o password provisional). En primer lugar porque, a partir de enero de 2021, los navegadores no permitirán la ejecución online de recursos digitales realizados en Flash. En segundo lugar, porque debido al conocimiento, anunciado años atrás, de este hecho todos se han integrado en el proyecto MATE.TIC.TAC. offline, que ya no es gratuito y se puede adquirir en nuestra tienda online (matetictac.com) y que no depende de ningún navegador ni de
ResponderEliminarla discontinuación de Flash...
Saludos.