Son escasísimos los contenidos educativos digitales multimedia que tratan aspectos topológicos básicos.
Muchos recordamos, aunque de manera vaga e indefinida, que una vez en la escuela se nos propuso resolver el reto de la “casita” (o “sobre de carta” si se prefiere). Se trataba de realizar el dibujo de un solo trazo, sin levantar el lápiz del papel y sin dibujar un mismo segmento dos veces…
Probablemente una gran mayoría de personas, incluso una mayoría de docentes, no hayamos sido conscientes de los momentos de acercamiento a cuestiones que tienen relación con esta rama de la geometría denominada topología, sobre todo de los aspectos lúdicos de la misma.
 |
| "Casita" o "sobre de carta" |
El sencillo reto de la “casita” enlaza directamente con el famoso e histórico problema de los puentes de Königsberg, con el matemático Euler, con el nacimiento de la topología y de la potente teoría de grafos.
La aplicación que aquí ofrezco, organizada en torno a cuatro secciones o apartados, hace posible de manera experimental, creativa y lúdica, que comprender y argumentar razonadamente sobre el problema de los puentes de Königsberg (y variantes del mismo) así como crear y dar respuesta a otros problemas análogos más complejos sea una tarea de matemáticas relevante al alcance de niños de Primaria, a la par que los familiariza con aspectos básicos de la topología.
En el apartado RETOS se ilustra de manera dinámica lo que se entiende por “recorrido de un solo trazo” y se propone, a modo de retos, una veintena de figuras que pueden ser recorridas de un solo trazo, cada una de ellas de múltiples maneras (aquí soluciones). Se trata, pues, de una actividad de naturaleza divergente, creativa… El ordenador permite comprobar lo correcto o no del trazado realizado por el usuario en cada caso, es decir, de la solución concreta dada por él. Los retos propuestos permitirán intuir y descubrir la existencia de ciertos patrones o regularidades. Así, por ejemplo, la aplicación redibuja el trazado realizado por el usuario en el mismo sentido que éste lo hizo y en sentido contrario evidenciando de manera visual y dinámica que toda solución es doble. Pronto el usuario descubre que unas figuras tienen solución comenzando en uno cualquiera de sus vértices (y terminando en el mismo) y otras, en cambio, exigen comenzar y terminar en vértices concretos. ¿Por qué?
 |
| Las veinte figuras propuestas (de diferente dificultad) |
 |
| Comprobación de un trazado solución correspondiente a la figura propuesta número 9 |
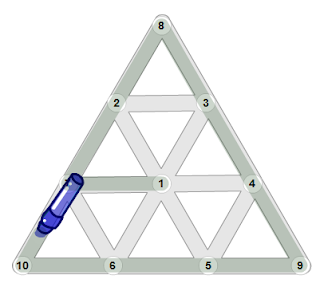 |
| Trazado de una solución (1-7-2-8-3-4-9-5-6-10-7-6-1-5-4-1-3-2-1) |
El apartado TEORÍA se aprovecha para introducir e ilustrar dinámicamente conceptos topológicos básicos relacionados con los retos propuestos y sus soluciones, tales como: figuras topológicamente equivalentes, grafo, grafos topológicamente equivalentes, vértices o nodos, segmentos o arcos, regiones, orden de un nodo, nodo par, nodo impar,…
También se utiliza el apartado TEORÍA para llevar al alumno al descubrimiento o comprobación de unos cuantos resultados teóricos sencillos que son expresión de las regularidades que han podido ser experimentadas y que permiten determinar si un grafo va a tener o no solución. Se muestra de manera dinámica una familia de grafos generados “de un solo trazo” con un espirógrafo configurable, se pregunta sobre las características comunes de estas figuras así generadas; se muestran colecciones de figuras para que el usuario determine si tienen o no solución, etc... Esta teoría está perfectamente al alcance de niños/as de 9-10 años en adelante y es la que permitirá comprobar que el originario problema de los puentes de Königsberg no tiene solución.
Para completar aspectos no tocados en esta aplicación o bien para verlos desde otro punto de vista, se enlaza con algunas aplicaciones para Educación Primaria correspondientes al Proyecto Canals (de Hernán Darío Alzate: "Redes I", "Redes II" y "Topología" ; de Diego Luis Feria Gómez: "Posiciones relativas entre líneas" ) a vídeos de YouTube sobre esta temática y a diferentes documentos digitales online.
 |
| "Los siete puentes de Königsberg" |
En el apartado TALLER el usuario puede crear sus propios grafos colocando nodos y arcos en la zona de diseño tal y como desee. El ordenador evalúa si el grafo realizado tiene o no solución y por qué… Además sugiere y permite la simulación o modelado del problema de los puentes de Königsberg y variantes del mismo…
Por último, y esto puede que sólo interese a desarrolladores de contenidos educativos digitales, la aplicación muestra un amplio abanico de maneras diferentes de abordar el trazado interactivo de líneas rectas y curvas...
(Se agradecen los comentarios)


Me ha gustado mucho esta aplicación para trabajar la Topología, y claro que se puede trabajar en Primaria, además de como tu dices, ser actividades creativas. Ahora, por tu generosidad y buen hacer, lo tenemos organizado e interactivo.
ResponderEliminarNo tengo dudas de que la voy a utilizar en clase.
Un saludo, Mariángeles
Es excelente la aplicacion, y el post tambien.
ResponderEliminarGracias por vuestros comentarios.
EliminarFelicitaciones profesor Juan.
ResponderEliminarMe encanta revisar su página.
Saludos desde Colombia.
Gracias, CbA. ¿Cómo es que abadonaste "Orden & Caos"?
Eliminar