Jugando con la trama de puntos interactiva...

Comprobando el correcto funcionamiento de la aplicación Trama de puntos interactiva, me encontré con una situación que llamó poderosamente mi atención. Aunque lo que voy a exponer a continuación excede el nivel al que suele ceñirse este blog, puede que algunos/as lectores/as encuentren útiles algunas de la reflexiones que aquí expongo.

Ante todo, lo que sigue es consecuencia directa de la posibilidad de "manipulación libre" que implemento en la gran mayoría de las aplicaciones que diseño, lo cual les confiere un enorme potencial para favorecer "el aprendizaje por descubrimiento".

 

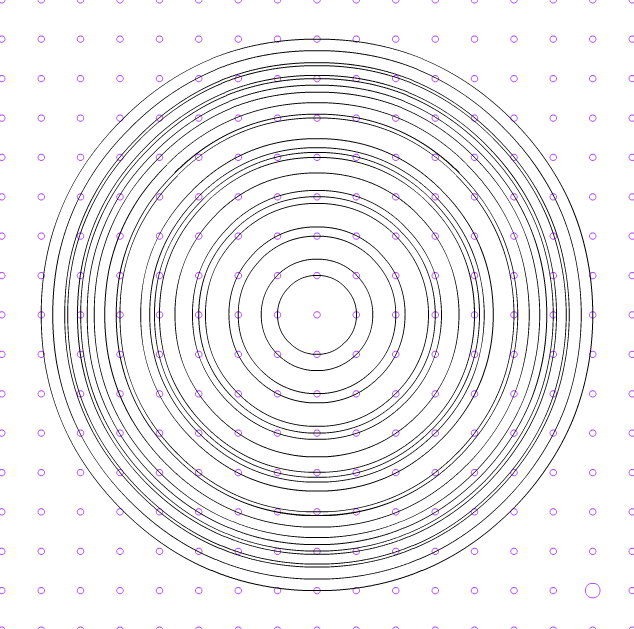
La situación tiene que ver con la trama ortométrica y un problema de geometría euclídea. Elegí un punto como centro y comencé a trazar circunferencias concéntricas de manera que la sucesión de éstas fuera alcanzando los puntos de la trama sin dejar ninguno de ellos sin estar contenido en alguna circunferencia.

 

Lo que me llamó poderosamente la atención es que la serie de las circunferencias obtenidas parece no seguir ningún patrón, a pesar del orden tan patente que organiza los puntos de la trama. Se pueden encontrar dos circunferencias concéntricas consecutivas de radios muy próximos y la siguiente distanciarse "bastante" de las anteriores...

 

Evidentemente, si tomamos como unidad la distancia mínima entre dos puntos próximos de la trama (que podemos considerar dentro de un plano, es decir, infinita), la primera circunferencia tiene de radio 1, la segunda tiene de radio (raíz cuadrada de 2),... y la diferencia entre los radios de dos circunferencias consecutivas va a ser siempre menor que 1.

 

Me fijé en diferentes variables (número de puntos de la trama pertenecientes a cada circunferencia, radio de las circunferencias trazadas, coordenadas de los puntos,…)

 

Para la determinación de la primera variable, basta realizar una adecuada y exacta construcción de las circunferencias (para ello la trama de puntos interactiva es ideal aunque limitada) y con saber contar.

Así, la serie del número de puntos de la trama perteneciente a cada circunferencia es :

 4, 4, 4, 8, 4, 4, 8, 8, 4, 8, 4, 8, 12, 8, …. 

Parece ser que una circunferencia cualquiera de esta serie de circunferencias concéntricas siempre va a tener un número de puntos de la trama múltiplo de 4. Pero, ¿presenta esta serie alguna regularidad o patrón que permita obtener la fórmula que nos dé el número de puntos de la trama perteneciente a una circunferencia cualquiera en función  del número de orden de ésta? ¿Se podrá encontrar una circunferencia en la serie que contenga un número de puntos de la trama que sea múltiplo de 4 y tan grande como deseemos?

 

Aunque no lo he investigado a fondo, yo personalmente no encuentro ningún patrón que permita determinar con exactitud la serie de números anterior.

 

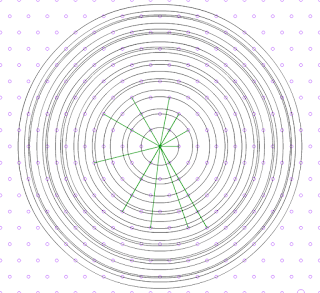
Para la determinación de la serie ordenada de números correspondientes a los radios de las circunferencias, se necesita hacer uso del famoso teorema de Pitágoras ( que es ya un contenido de Educación Secundaria). Aplicando este teorema se obtiene con facilidad la serie de radios:

(Aunque las raíces cuadradas de los cuadrados perfectos - en verde- son números naturales, he preferido unificar, en forma de raíces, la presentación de la serie)

La situación anterior se puede formular de otras maneras equivalentes: Dada una circunferencia con centro en el origen de coordenadas cartesianas, determinar los radios de las circunferencias que tienen al menos 4 puntos cuyas coordenadas son números enteros. Así la circunferencia de radio 1 tendría 4 puntos de coordenadas enteras [(0,1), (-1,0),(0,-1) y (1,0)]. 

Con un radio mayor que 1 y menor que raíz de 2 no existe ninguna circunferencia con centro en el origen (0,0) que tenga puntos con coordenadas enteras...

¿Habrá alguna circunferencia con centro en el origen de coordenadas que tenga un número (múltiplo de 4) tan grande como se desee de puntos con coordenadas enteras?...

¿Cómo determinar los radios de las circunferencias que tienen al menos cuatro puntos de coordenadas enteras? Yo no soy capaz de encontrar ningún patrón en la serie de radios de estas circunferencias (no tiene por qué haberlo). 

Por analogía, se puede plantear la misma situación en la trama isométrica. Tampoco encuentro ningún patrón a excepción de que los puntos de la trama contenidos en cada circunferencia son múltiplos de 6 : 6, 6, 6, 12, 6, 6, 12, 6, 12, 12, 6, 6, ......., 18,...

Casi con toda seguridad, esta situación ya habrá sido matematizada anteriormente por alguien. Yo lo desconozco y, por si acaso, la dejo aquí, como problema abierto a la comunidad de "matemáticos"...

(Agradecería mucho cualquier información, enlace o comentario al respecto)

Algunas reflexiones relacionadas con lo anterior:

1.- La búsqueda de patrones o regularidades debe ser el motor fundamental de la actividad matemática en cualquier nivel. Se puede llevar a cabo desde Educación Infantil, constituye una valiosa fuente de aprendizaje y es imprescindible en una matemática enfocada al aprendizaje por descubrimiento. Es un contenido procedimental general de carácter transversal con respecto a todos los contenidos de la Matemática y de las otras disciplinas.

Ejemplo: Hoy mismo mis alumnos/as de 5º han ampliado considerablemente los criterios de divisibilidad que se dan en el libro de texto (por 2, por 3, por, 5, por 9 y por 10) con otros descubiertos y expresados por ellos (por 6, por 15, por 20, por 25, por 50, por 100, por 200, por 250, por 500,...) a partir de la visualización en la PDI de series de múltiplos de los números anteriores.

2.- No sólo existen patrones numéricos. Es fundamental trabajar los patrones geométricos, porque Geometría y Numeración están estrechamente relacionados, como es el caso de la situación con la que he iniciado este post, y porque son especialmente atractivos e intuitivos y favorecen la captación y expresión de las regularidades... 
( Ver Trama de puntos interactiva  y  Regularidades en matemáticas. Patrones)

3.- La propia matemática se constituye, así, en un contexto ideal en el que podemos plantear numerosas situaciones atractivas para descubrir patrones y regularidades en relación con cada uno de los contenidos que se tratan en el currículo de matemáticas.